Ідеальна кільцева в'язанка
Ідеальна кільцева в'язанка (ІКВ) — це циклічна послідовність ( ,,…,) чисел, на якій всі можливі кільцеві суми вичерпують значення чисел натурального ряду від 1 до S n=n(n — 1). Винахід Володимира Різника.
Властивості
Кільцевою сумою називається сума будь-якої кількості (від 1 до n-1) послідовно розміщених елементів циклічної n-послідовності. Наприклад, циклічна послідовність (1,3,2,7), що на рис. 1, є ідеальною кільцевою в'язанкою, оскільки чотири (n=4) її елементи перелічують всі числа натурального ряду від 1 до , утворених рівно одним (R=1) способом обрання початкового та останнього елементів цієї послідовності, що додаються:
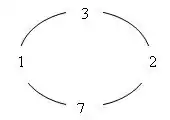
| 1, |
| 2, |
| 3, |
| 4=1+3, |
| 5=3+2, |
| 6=1+3+2, |
| 7, |
| 8=7+1, |
| 9=2+7, |
| 10=2+7+1, |
| 11=7+1+3, |
| 12=3+2+7, |
| 13=1+3+2+7. |
Цей ряд можна продовжити, обираючи перший елемент для початку відліку та обходячи кільцеву схему більше одного разу, наприклад: 15=2+7+1+3+2 тощо.
Різновиди ІКВ
Повні сім'ї деяких ІКВ для n ≤ 13
| n | R | ІКВ |
|---|---|---|
| 4 | 1 | 1 3 2 7 1 2 6 4 |
| 4 | 2 | 1 1 2 3 |
| 5 | 1 | 1 3 10 2 5 |
| 5 | 2 | 1 1 2 3 4 |
| 6 | 1 | 1 2 5 4 6 13 1 2 7 4 12 5 1 3 2 7 8 10 1 3 6 2 5 14 1 7 3 2 4 14 |
| 6 | 3 | 1 1 2 1 2 4 |
| 7 | 3 | 1 1 2 1 3 2 5 |
| 8 | 1 | 1 2 10 19 4 7 9 5 1 3 5 11 2 12 17 6 1 3 8 2 16 7 15 5 1 4 2 10 18 3 11 8 1 6 12 4 21 3 2 8 |
| 8 | 4 | 1 1 1 2 2 1 3 4 |
| 9 | 1 | 1 2 4 8 16 5 18 9 10 1 4 7 6 3 28 2 8 14 1 6 4 24 13 3 2 12 8 1 11 8 6 4 3 2 22 16 |
| 9 | 2 | 1 2 4 10 7 1 4 6 2 1 25 4 2 3 1 12 7 |
| 9 | 4 | 1 1 1 2 2 5 1 3 3 |
| 9 | 6 | 1 1 1 1 1 2 2 1 3 1 1 1 1 2 1 1 3 2 |
| 10 | 1 | 1 2 6 18 22 7 5 16 4 10 1 3 9 11 6 8 2 5 28 18 1 4 2 20 8 9 23 10 3 11 1 4 3 10 2 9 14 16 6 26 1 5 4 13 3 8 7 12 2 36 1 6 9 11 29 4 8 2 3 18 |
| 10 | 5 | 1 1 1 2 2 5 1 2 1 3 |
| 11 | 5 | 1 1 1 2 2 1 3 1 3 2 6 |
| 12 | 1 | 1 2 9 8 14 4 43 7 6 10 5 24 1 2 12 31 25 4 9 10 7 11 16 5 1 2 14 4 37 7 8 27 5 6 13 9 1 2 14 12 32 19 6 5 4 18 13 7 1 38 9 5 19 23 16 13 2 28 6 1 3 12 34 21 2 8 9 5 6 7 25 1 3 23 24 6 22 10 11 18 2 5 8 1 4 7 3 16 2 6 17 20 9 13 35 1 4 16 3 15 10 12 14 17 33 2 6 1 4 19 20 27 3 6 25 7 8 2 11 1 4 20 3 40 10 9 2 15 16 6 7 1 5 12 21 29 11 3 16 4 22 2 7 1 7 13 12 3 11 5 18 4 2 48 9 1 8 10 5 7 21 4 2 11 3 26 35 1 14 3 2 4 7 21 8 25 10 12 26 1 14 10 20 7 6 3 2 17 4 8 41 1 15 5 3 25 2 7 4 6 12 14 39 1 22 14 20 5 13 8 3 4 2 10 31 |
| 12 | 6 | 1 1 1 1 2 2 1 3 1 3 2 5 |
| 13 | 4 | 1 1 2 1 3 5 1 3 2 5 2 8 6 1 1 3 7 6 4 2 2 1 2 3 1 7 |
Циклічна послідовність (1,1,2,3) є також ідеальною кільцевою в'язанкою, оскільки чотири (n=4) її елементи перелічують всі числа натурального ряду від 1 до , утворених рівно двома (R=2) різними способом обрання початкового та останнього елементів цієї послідовності:
| 1, 1 |
| 2, 2=1+1 |
| 3, 3=2+1 |
| 4=3+1, 4=1+1+2 |
| 5=2+3, 5=3+1+1 |
| 6=1+2+3, 6=2+3+1 |

Окрім того, з ІКВ, наприклад, з (1, 3, 2, 7) можна отримати будь-яке двомісне співвідношення від 1:12 до 12:1. Сума чисел цього ІКВ 1+3+2+7=13 може бути розбита на частини так, щоб у множині всіх можливих способів його розбиття отримати ряд двомісних пропорцій (рис. 2). Таких сум є безліч.
Багатовимірна ІКВ — це циклічна n-послідовність сумірних багатовимірних елементів, наприклад, t-вимірних векторів, множина усіх кільцевих вектор-сум яких, обчислених за відповідними модулями перелічує координати правильної t-вимірної решітки фіксоване число разів.
Кільцевою вектор-сумою називається сума будь-якої кількості (від 1 до n-1) послідовно розміщених t-вимірних векторів кільцевої n-послідовності. Прикладом двовимірної (t=2) ІКВ є циклічна послідовність векторів ((0,1), (0,2), (1,1)), де модулем (довжиною циклу) першої складової двовимірного вектора є =2, а другої — =3. Обчисливши всі кільцеві вектор-суми з урахуванням числових значень відповідних модулів, легко перевірити, що вони вичерпують множину координат двовимірної решітки 2×3:
Однією з необхідних умов існування t-вимірної ІКВ з параметрами n, R є вимога ( ,,…,)=1, де , , — розміри t-вимірної решітки, добуток числових значень яких дорівнює або . Теоретично доведено, що існує як завгодно багато ІКВ.
Будь-яка з наявних ідеальних в'язанок з ланцюжковою структурою — так звана «ідеальна лінійка Голомба» є частиною відповідної ІКВ. На відміну від ідеальної лінійки Голомба, існує нескінченно багато ІКВ.
Зв'язок із класичною теорією
Теорія ІКВ базується на окремих розділах комбінаторного аналізу, алгебричної теорії чисел та полів Ґалуа.
Застосування
ІКВ знаходять застосування в контрольно-вимірювальній техніці, інформаційних і комп'ютерних технологіях, електротехніці та радіофізиці, кібернетиці й логістиці.
Див. також
- Різник Володимир Васильович
- Ансамбль досконалих куторомірів
- Golomb Ruler
Посилання
- Наукова школа професора Різника
- V.V.Riznyk. Multi-dimensional systems based on perfect combinatorial models. Colloquium on Multidimensional Systems: Problems and Solutions.IEE, Savoy Place, London WC2R 0BL, UK, pp.5/1-5/4, January 1998.
- James David A., Magic circles.- Math.Mag..-1981, v.54, № 3, p.122-125.
- Volodymyr Riznyk, Perfect distribution phenomenon and the origin of the space-time harmony, Generative Art Conference (GA2001), Milan, Italy,2001.
- V.Riznyk, Application of Ideal Ring-Like Combinatorial Configurations for Modelling on Nonlinear Processes, Proceedings of the 5th Zittau Fuzzy Colloquium, Sept. 4-5, 1997, Zittau, Germany,1997, pp.115-117.
- V.Riznyk, Multidimensional Systems Based on Perfect Combinatorial Models, IEE, Multidimencional Systems:Problems and Solutions,London, UK, 1998, #225, pp.5/1-5/4.
- V.Riznyk, Perfect Distribution Phenomenon in Combinatorics and Its applications to System Optimization, 19-th IFIP TC7 Conference on System Modelling and Optimization, Cambridge, July 12-16, 1999, England.
- V.Riznyk, Perfect Structural Distribution Phenomenon in Mathematics, Technology and Nature, Proceedings of the 4th Congress and Exhibition od ISIS-Symmetry, Sept. 13-19, 1998, Haifa, Israel.
- А. К. Дьюдни, О линейках Коломба и их применении в радиоастрономии. -В мире науки(Scientific American), № 2, 1986, с.103-107.
- Різник В. В. Синтез оптимальних комбінаторних систем.-Львів, Вища школа, 1989. −168 с.
- А.с. СССР 429276, Способ дозирования веществ, Бюл.№ 19, 1974.
- Від таємниць симетрії до пізнання всеосяжної гармонії природи// Вісник НТШ. — 2008. — Число 40. — с. 30-33.