Ізометричні поверхні

Ізометричні поверхні — поверхні в евклідовому просторі або рімановому просторі такі, що між ними можна встановити взаємно однозначну точкову відповідність, за якої кожна спрямлена крива однієї з поверхонь має своїм образом також спрямлену криву і тієї ж довжини.

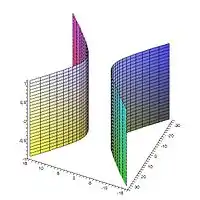
Ізометричні поверхні характеризуються ізометричною (попарною) відповідністю — ізометрією відносно внутрішніх метрик, індукованих на них метрикою осяжного простору.

Якщо ізометрія поверхонь тягне їх рівність, точніше, якщо для будь-якої поверхні $\Phi$ з деякого класу $\mathrm {K}$ , ізометричної поверхні $\Phi _{1}$ , просторові відстані між відповідними за ізометрією точками $\Phi$ і $\Phi _{1}$ рівні, то $\Phi _{1}$ називається однозначно визначеною, або для $\Phi _{1}$ має місце однозначна визначеність (внутрішньою метрикою) в класі $\mathrm {K}$ .

Теорема Гауса

Поверхні $\Phi$ і $\Phi _{1}$ називаються ізометричними, якщо існує взаємно однозначне відображення поверхні $\Phi$ на поверхню $\Phi _{1}$ , при якому відповідні криві на цих поверхнях мають однакові довжини.

Якщо регулярні поверхні $\Phi$ і $\Phi _{1}$ можна параметризувати так, що їх перші квадратичні форми будуть однакові, то поверхні ізометричні. Ізометричне відображення полягає у зіставленні точок з однаковими координатами.

Зворотньо, якщо поверхні $\Phi$ і $\Phi _{1}$ ізометричні, то вони можуть бути параметризовані так, що їх перші квадратичні форми будуть однакові.

Властивості

Приклад ізометричної поверхні — сукупність поверхонь, отриманих згинанням даної поверхні.

Рівні поверхні — ізометричні. Зворотне не завжди вірно. Наприклад, область $0<x<{\tfrac {\pi }{2}}$ , $0<y<1$ на координатній площині $XOY$ ізометрична області на циліндрі $x^{2}+y^{2}=1$ , що визначається умовами: $0<Z<1,X>0,Y>0.$

Для доказу достатньо помітити, що вказана область на циліндрі допускає параметризацію: $x=\cos u,y=\sin u,z=v,0<u<{\tfrac {\pi }{2}},0<v<1.$

Лінійний елемент циліндру, що відповідає такій параметризації, є $du^{2}+dv^{2}.$ Звідси видно, що відображення $x=u,y=v$ , ізометричне.

Так як кути між кривими на поверхні і площа поверхні визначається першою квадратичною формою, то при ізометричному відображенні зберігаються кути між кривими і площами, то є відповідні криві ізометричних поверхонь утворюють однакові кути, а відповідні області мають однакові площі.

Вигинання поверхні

Вигинання неперервно пов'язано з ізометричними поверхнями. Вигинанням поверхні називається така неперервна її деформація, за якої довжини кривих на поверхні не змінюються. Наочне уявлення про вигинання може дати вигинання аркуша паперу (за умови, що папір нерозтяжний; тому довжина кожної дуги будь-якої лінії, проведеної на папері, залишається незмінною).

Так як при вигинанні поверхні довжини кривих не змінюються і, отже, поверхня в будь-який момент вигинання ізометрична початковій поверхні, то при відповідній параметризації перша квадратична форма при вигинанні поверхні не змінюється.

Серед поверхонь існують поверхні, що не допускають неперервних вигинань. Такі, наприклад, всі замкнені опуклі поверхні. Одна з теорем цієї області — теорема Гауса:

При вигинанні поверхні добуток її головних кривин (повна кривина) в кожній точці залишається незмінним.

З цієї теореми випливає, що ніякий шматок сфери за допомогою вигинання не можна перетворити на шматок сфери іншого радіуса або надати йому пласку форму.

Сукупність геометричних факторів, що відносяться до поверхні, які можна отримати за допомогою її першої квадратичної форми, складають так звану внутрішню геометрію поверхні. Таким чином, якщо поверхня $\Phi$ отримується з поверхні $\Phi 1$ шляхом вигинання, то внутрішні геометрії цих поверхонь однакові.

Доведено, що кожна замкнена опукла поверхня (наприклад, ціла сфера, цілий еліпсоїд) не може вигинатися; якщо ж з такої поверхні вирізати як завгодно малий шматок, то частина, що залишилася, буде допускати вигинання. Доведення отримано завдяки роботам німецького математика С. Кон-Фосена і радянських математиків О. Д. Александрова і О. В. Погорєлова.

Див. також

Література

Математична енциклопедія. — М.: Радянська енциклопедія. И. М. Виноградов 1977–1985

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.