Алгоритм Грувера

Хоча мета алгоритму Грувера зазвичай описується як «пошук в базі даних», можна більш точно описати його як «інвертування функції». Насправді, так як «пророча машина» неструктурованої бази даних вимагає, хоча б лінійної складності, алгоритм не може бути використаний для реальних баз даних.[1] Грубо кажучи, якщо функцію ${\displaystyle y=f(x)}$ можна оцінити на квантовому комп'ютері, алгоритм Грувера обчислює ${\displaystyle x}$ за заданим ${\displaystyle y}$. Інверсія функція пов'язана з пошуком бази даних, тому що ми могли б придумати функцію, яка виробляє одне конкретне значення ${\displaystyle y}$ (наприклад «істинно»), якщо ${\displaystyle x}$ відповідає потрібному запису в базі даних, і інше значення ${\displaystyle y}$ («хибно») для інших значень ${\displaystyle x}$.

Алгоритм Грувера також може бути використаний для знаходження медіани і середнього арифметичного числового ряду.[2] Крім того, він може застосовуватися для вирішення NP-повних задач шляхом вичерпного пошуку серед безлічі можливих рішень. Це може спричинити значний приріст швидкості в порівнянні з класичними алгоритмами, хоча і не надаючи «поліноміального рішення» в загальному вигляді. Алгоритм може бути додатково оптимізовано, якщо існує більше, ніж один елемент. що збігається і число збігів відомо заздалегідь.

Розглянемо невпорядовану базу даних з ${\displaystyle N}$ записів. Алгоритм вимагає ${\displaystyle N}$-вимірний простір станів ${\displaystyle {\mathcal {H}}}$, в яких можуть перебувати ${\displaystyle n=\lceil log_{2}N\rceil }$ кубітів. Розглянемо задачу визначення індексу записи бази даних, яка задовольняє деяким заданим критеріям. Нехай f — функція, яка показує всі записи бази даних 0 або 1, де f(x) = 1 тоді і тільки тоді, коли x відповідає критерію пошуку (x = ω). Ми отримали доступ до підпрограми (так званий оракул або пророча машина) у вигляді унітарного оператора U_ω, який діє в такий спосіб:

${\displaystyle {\begin{cases}U_{\omega }|x\rangle =-|x\rangle &{\text{for }}x=\omega {\text{, that is, }}f(x)=1,\\U_{\omega }|x\rangle =|x\rangle &{\text{for }}x\neq \omega {\text{, that is, }}f(x)=0.\end{cases}}}$

Альтернативне визначення U_ω може виникнути через припущення про наявність додаткової системи кубіта (як у квантовій системі, яка зображена нижче). Операція потім представляє собою умовне інвертування (NOT), обумовлене величиною f(x) у головній системі:

${\displaystyle {\begin{cases}U_{\omega }|x\rangle |y\rangle =|x\rangle |\neg y\rangle &{\text{for }}x=\omega {\text{, that is, }}f(x)=1,\\U_{\omega }|x\rangle |y\rangle =|x\rangle |y\rangle &{\text{for }}x\neq \omega {\text{, that is, }}f(x)=0,\end{cases}}}$

або коротко,

${\displaystyle U_{\omega }|x\rangle |y\rangle =|x\rangle |y\oplus f(x)\rangle .}$

Це природний спосіб реалізувати бінарну операцію з використанням методу зворотного обчислення. Зверніть увагу, що якщо кубіт знаходиться в стані ${\displaystyle |-\rangle ={\frac {1}{\sqrt {2}}}{\big (}|0\rangle -|1\rangle {\big )}=H|1\rangle }$, ефективна робота цього оператору NOT стає еквівалентна вихідній формі:

${\displaystyle {\begin{aligned}U_{\omega }{\big (}|x\rangle \otimes |-\rangle {\big )}&={\frac {1}{\sqrt {2}}}\left(U_{\omega }|x\rangle |0\rangle -U_{\omega }|x\rangle |1\rangle \right)\\&={\frac {1}{\sqrt {2}}}\left(|x\rangle |f(x)\rangle -|x\rangle |1\oplus f(x)\rangle \right)\\&={\begin{cases}{\frac {1}{\sqrt {2}}}\left(|x\rangle |1\rangle -|x\rangle |0\rangle \right)=-|x\rangle \otimes |-\rangle &{\text{if }}f(x)=1,\\{\frac {1}{\sqrt {2}}}\left(|x\rangle |0\rangle -|x\rangle |1\rangle \right)=|x\rangle \otimes |-\rangle &{\text{if }}f(x)=0\end{cases}}\end{aligned}}}$

У будь-якому випадку, наша мета полягає в тому, щоб визначити індекс ${\displaystyle |\omega \rangle }$.

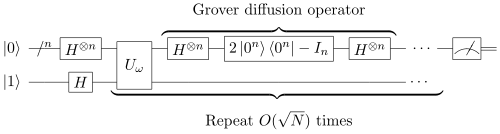
Етапи роботи алгоритму Грувера наведені нижче. Позначимо через ${\displaystyle |s\rangle }$ рівномірну суперпозицію по всім станам

${\displaystyle |s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=0}^{N-1}|x\rangle .}$

Тоді оператор

${\displaystyle U_{s}=2\left|s\right\rangle \left\langle s\right|-I}$

вважатимемо, як оператор дифузії Грувера.

Власне алгоритм:

1. Ініціалізуємо стан систем
   ${\displaystyle |s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=0}^{N-1}|x\rangle .}$
2. Виконуємо наступні «ітерації Грувера» ${\displaystyle r(N)}$ раз. Функція є асимптотичною ${\displaystyle O({\sqrt {N}})}$ , як описано нижче.
   1. Застосовуємо оператор ${\displaystyle U_{\omega }}$.
   2. Застосовуємо оператор ${\displaystyle U_{s}}$.
3. Визначаємо значення Ω. Результат вимірювання буде власне λ_ω з ймовірністю, що наближається до 1 для N "1. З λ_ω може бути отримано ω.

Попереднє спостереження, паралельно з нашим визначенням

${\displaystyle U_{s}=2|s\rangle \langle s|-I,}$

є ${\displaystyle U_{\omega }}$, що може бути виражено альтернативним шляхом:

${\displaystyle U_{\omega }=I-2|\omega \rangle \langle \omega |.}$

Іншими словами, обидва перетворення мають перетворення типу Хаусхолдера. Для доказу цього достатньо, щоб перевірити, як ${\displaystyle U_{\omega }}$ діє на основні стани:

${\displaystyle {\begin{aligned}(I-2|\omega \rangle \langle \omega |)|\omega \rangle &=|\omega \rangle -2|\omega \rangle \langle \omega |\omega \rangle =-|\omega \rangle =U_{\omega }|\omega \rangle ,\\(I-2|\omega \rangle \langle \omega |)|x\rangle &=|x\rangle -2|\omega \rangle \langle \omega |x\rangle =|x\rangle =U_{\omega }|x\rangle &&\forall x\neq \omega .\end{aligned}}}$

Наступні обчислення показують, що відбувається в першій ітерації::

${\displaystyle {\begin{aligned}\langle \omega |s\rangle &=\langle s|\omega \rangle ={\tfrac {1}{\sqrt {N}}},\\\langle s|s\rangle &=N{\tfrac {1}{\sqrt {N}}}\cdot {\tfrac {1}{\sqrt {N}}}=1,\\U_{\omega }|s\rangle &=(I-2|\omega \rangle \langle \omega |)|s\rangle =|s\rangle -2|\omega \rangle \langle \omega |s\rangle =|s\rangle -{\tfrac {2}{\sqrt {N}}}|\omega \rangle ,\\U_{s}\left(|s\rangle -{\tfrac {2}{\sqrt {N}}}|\omega \rangle \right)&=\left(2|s\rangle \langle s|-I\right)\left(|s\rangle -{\tfrac {2}{\sqrt {N}}}|\omega \rangle \right)=2|s\rangle \langle s|s\rangle -|s\rangle -{\tfrac {4}{\sqrt {N}}}|s\rangle \langle s|\omega \rangle +{\tfrac {2}{\sqrt {N}}}|\omega \rangle \\&=2|s\rangle -|s\rangle -{\tfrac {4}{\sqrt {N}}}\cdot {\tfrac {1}{\sqrt {N}}}|s\rangle +{\tfrac {2}{\sqrt {N}}}|\omega \rangle =|s\rangle -{\tfrac {4}{N}}|s\rangle +{\tfrac {2}{\sqrt {N}}}|\omega \rangle \\&={\tfrac {N-4}{N}}|s\rangle +{\tfrac {2}{\sqrt {N}}}|\omega \rangle .\end{aligned}}}$

Варто відзначити окремий випадок при N = 4 з одним визначеним станом. Це ${\displaystyle U_{s}U_{w}|s\rangle =|\omega \rangle }$ означає, що в одному застосуванні ітератора Грувера зазначений стан повертається.

Після застосування операторів ${\displaystyle U_{\omega }}$ і ${\displaystyle U_{s}}$, квадрат амплітуди запитуваного елемента збільшиться з ${\displaystyle \left|\langle \omega |s\rangle \right|^{2}={\tfrac {1}{N}}}$ до ${\displaystyle \left|\langle \omega |U_{s}U_{\omega }|s\rangle \right|^{2}=\left|{\tfrac {1}{\sqrt {N}}}\cdot {\tfrac {N-4}{N}}+{\tfrac {2}{\sqrt {N}}}\right|^{2}={\tfrac {(3N-4)^{2}}{N^{3}}}=9\left(1-{\tfrac {4}{3N}}\right)^{2}\cdot {\tfrac {1}{N}}}$.

Алгоритм Грувера вимагає «квантового передбачення» оператора ${\displaystyle U_{\omega }}$, який може визначати рішення проблеми пошуку і дати їм негативний знак. Для того, щоб зберегти загальний алгоритм пошуку, ми залишимо внутрішню роботу «оракула» як чорний ящик, але пояснимо, як перевертається знак. Оракул — це функція ${\displaystyle f}$, яка повертає ${\displaystyle f(x)=1}$ if ${\displaystyle |x\rangle }$, якщо це рішення задачі пошуку і ${\displaystyle f(x)=0}$ в іншому випадку. Унітарний оператор передбачення працює для двох кубітів:

${\displaystyle |x\rangle |q\rangle \,{\overset {U_{\omega }}{\longrightarrow }}\,|x\rangle |q\oplus f(x)\rangle ,}$

де ${\displaystyle |x\rangle }$ — індекс кубіта і оракул кубіта.

Як завжди, ${\displaystyle \oplus }$ позначає додавання за модулем 2. Операція перевертає оракул кубіта, якщо ${\displaystyle f(x)=1}$ і залишає його без змін в іншому випадку. В алгоритмі Грувера ми хочемо обернути знак стану ${\displaystyle |x\rangle }$, якщо він визначає рішення. Це досягається шляхом установки оракула кубіту в стані ${\displaystyle (|0\rangle -|1\rangle )/{\sqrt {2}}}$, який перевертається до ${\displaystyle (|1\rangle -|0\rangle )/{\sqrt {2}}}$ if ${\displaystyle |x\rangle }$, якщо це рішення:

${\displaystyle |x\rangle \left(|0\rangle -|1\rangle \right)/{\sqrt {2}}\,{\overset {U_{\omega }}{\longrightarrow }}\,(-1)^{f(x)}|x\rangle \left(|0\rangle -|1\rangle \right)/{\sqrt {2}}.}$

Ми розглядаємо ${\displaystyle |x\rangle }$, як обернене, таким чином оракул кубіта не змінюється, тому відповідно до визначення оракула кубітів, як правило, не згадується в описі алгоритму Грувера. Таким чином, операція оракула ${\displaystyle U_{\omega }}$ просто записується у вигляді

${\displaystyle |x\rangle \,{\overset {U_{\omega }}{\longrightarrow }}\,(-1)^{f(x)}|x\rangle .}$

Припустимо, рівняння (1) має корені. Класичний алгоритм вирішення такого завдання (лінійний пошук), очевидно, вимагає ${\displaystyle O({\tfrac {N}{l}})}$ звернень до ${\displaystyle f}$ для того, щоб вирішити задачу з імовірністю ½. Алгоритм Грувера дозволяє вирішити задачу пошуку за час ${\displaystyle O({\sqrt {\tfrac {N}{l}}})}$, тобто близько квадратного кореня з класичного, що є величезним прискоренням. Доведено, що Алгоритм Грувера є оптимальним в наступних випадках:

• константу ${\displaystyle {\tfrac {\pi }{4}}}$ не можна поліпшити.
• Більшого квантового прискорення, ніж квадратичне, не можна отримати.

Алгоритм Грувера є приклад масової задачі, що залежить від оракула. Для більш приватних завдань вдається отримати більше квантове прискорення. Наприклад, алгоритм факторизації Шора дає експонентний виграш в порівнянні з відповідними класичними алгоритмами.

Те, що f задана у вигляді чорного ящика, ніяк не впливає в загальному випадку на складність як квантових, так і класичних алгоритмів. Знання «пристрою» функції f (наприклад, знання задає її схеми з функціональних елементів) в загальному випадку ніяк не може допомогти у вирішенні рівняння (1). Пошук в базі даних співвідноситься зі зверненням функції, яка приймає певне значення, якщо аргумент x відповідає шуканої записи в базі даних.

• Алгоритм пошуку екстремуму цілочисельної функції (P. Hoyer і ін.). Шукається найбільше значення функції ${\displaystyle f:\ \{0,1\}^{n}\rightarrow \{0,1\}^{n}}$. Квантовий алгоритм знаходить максимум ${\displaystyle O({\sqrt {N}})}$ звернень до f.
• Алгоритм структурного пошуку (Farhi, Gutman). Шукається розв'язок рівняння (1) при додатковій умові ${\displaystyle g(x_{1})=1}$, де ${\displaystyle x=x_{1}x_{2}}$${\displaystyle x=x_{1}x_{2}}$ — розбиття рядка ${\displaystyle x}$ на два рядки однакової довжини. Алгоритм має складність порядку квадратного кореня з класичного часу.
• Алгоритм пошуку співпадаючих рядків в базі даних (Амбайніс). Шукається пара різних аргументів ${\displaystyle x_{1}\neq x_{2}}$, на яких функція ${\displaystyle f:\ \{0,1\}^{n}\rightarrow \{0,1\}^{n}}$ приймає одне і те ж значення. алгоритм вимагає ${\displaystyle O(N^{3/4})}$ звернень до f.

Безперервні версії алгоритму Грувера

• Нехай гамільтоніан квантової системи має вигляд ${\displaystyle H=H_{1}+H_{2}}$ , де ${\displaystyle \exp(iH_{1})}$  і  ${\displaystyle \exp(iH_{2})}$ являють собою оператори ${\displaystyle I_{\tilde {0}}}$ і ${\displaystyle I_{\tilde {0}}}$ відповідно. Тоді безперервна унітарна еволюція з гамільтоніаном ${\displaystyle H}$, починаючи з ${\displaystyle |{\tilde {0}}\rangle }$, приводить до ${\displaystyle |x_{tar}\rangle }$. Складність такого безперервного аналога алгоритму Грувера точно та ж, що і для дискретного випадку.
• Адіабатичний варіант алгоритму Грувера. Повільна еволюція основного стану типу ${\displaystyle |{\tilde {0}}\rangle }$ під дією гамільтоніана, залежить від f , згідно адіабатичній теоремі, за час порядку ${\displaystyle {\sqrt {N}}}$ веде до стану ${\displaystyle |x_{tar}\rangle }$.

Відомо, що алгоритм Грувера є оптимальним. Тобто, будь-який алгоритм, який отримує доступ до бази даних тільки за допомогою оператора U_ω має застосовувати U_ω принаймні, стільки раз алгоритм Грувера.[3] Цей результат важливий для розуміння меж квантових обчислень.

Якщо проблема пошуку в Грувера мала розв'язок з log^c N застосувань U_ω, що означало б, що NP міститься в BQP, шляхом перетворення проблем в NP в пошукових завдань Грувер-типу. Оптимальність алгоритму Грувера передбачає (але не доводить), що NP не міститься в BQP.

Число ітерацій для k записів, π(N/k)^1/2/4, також є оптимальним.[4]

В базах даних, які не представлені в явному вигляді оракул викликається для оцінки елемента по його індексу, при цьому читання елементів повної бази даних один за одним і перетворення його в доступне подання може зайняти набагато більше часу, ніж пошук Грувера. Для врахування таких ефектів, алгоритм Грувера можна розглядати як рішення рівняння або задовольняють обмеження. У таких використаннях, оракул є способом перевірити обмеження і не пов'язаний з алгоритмом пошуку. Це поділ, як правило, запобігає алгоритмічній оптимізації, в той час як звичайні алгоритми пошуку часто покладаються на такі оптимізації і уникнути повного перебору. Ці та інші міркування з приводу використання алгоритму Грувера обговорюються в статті Віамонте, Маркова та Хеєса.[5]

• Алгоритм Шора
• Алгоритм з оракулом
• Квантові обчислення

• Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212
• Grover L.K.: From Schrödinger's equation to quantum search algorithm, American Journal of Physics, 69(7): 769—777, 2001. Pedagogical review of the algorithm and its history.
• Grover L.K.: QUANTUM COMPUTING: How the weird logic of the subatomic world could make it possible for machines to calculate millions of times faster than they do today The Sciences, July/August 1999, pp. 24–30.
• Nielsen, M.A. and Chuang, I.L. Quantum computation and quantum information. Cambridge University Press, 2000. Chapter 6.
• What's a Quantum Phone Book?, Lov Grover, Lucent Technologies
• Grover's Algorithm: Quantum Database Search, C. Lavor, L.R.U. Manssur, R. Portugal
• Grover's algorithm on arxiv.org
• Davy Wybiral. Quantum Circuit Simulator. Архів оригіналу за 16 січня 2017. Процитовано 13 січня 2017.
• Craig Gidney (5 березня 2013). Grover's Quantum Search Algorithm.
• François Schwarzentruber (18 травня 2013). Grover's algorithm.
• Alexander Prokopenya. Quantum Circuit Implementing Grover's Search Algorithm. Wolfram Alpha.
• Hazewinkel, Michiel, ред. (2001). Quantum computation, theory of. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
• Roberto Maestre (11 травня 2018). Grover's Algorithm implemented in R and C.