Кубіт

Основні одиниці; вимірювання інформації
	біт (двійкова); нат (основа e); гартлі (десяткова); кубіт (квантова);

У теорії квантових обчислень кубіт або квантовий біт (англ. quantum bit, qubit) — одиниця квантової інформації, квантовий аналог біта.

Кубіт — це дворівнева квантовомеханічна система, наприклад, поляризація окремого фотона, яка може бути вертикальною або горизонтальною. В класичній системі біт завжди прийматиме одне з двох значень, але квантова механіка дозволяє кубітові перебувати в стані суперпозиції. Ця властивість кубіта є базисом для всієї теорії квантових обчислень.

Стани кубіта

Представлення кубіта за допомоги сфери Блоха. Амплітуди ймовірності дорівнюють

a=\cos \left({\frac {\theta }{2}}\right),

b=e^{i\phi }\sin \left({\frac {\theta }{2}}\right).

На відміну від звичайного елемента, біта, який може приймати значення 0 та 1, кубіт може знаходитися в будь-якій суперпозиції цих двох станів. Лінійна суперпозиція базисних станів є чистим станом кубіта. Тому хвильова функція кубіта може бути записаною у вигляді кет-вектора, який є лінійною комбінацією $|0\rangle$ і $|1\rangle$ :

\psi =a|0\rangle +b|1\rangle ,

де a і b — комплексні числа, які задовільняють умові нормування

|a|^{2}+|b|^{2}=1.

При вимірюванні значення кубіта можна зафіксувати один із двох станів $|0\rangle$ і $|1\rangle$ , як і для звичайного біта, причому ймовірність отримати на виході стан $|0\rangle$ дорівнює $|a|^{2}$ , а стан $|1\rangle$ — $|b|^{2}$ . Перевага використання кубіта в тому, що при виконанні дій над кубітами одночасно обчислюються усі можливі значення виразів.

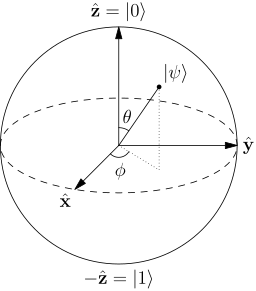
Сфера Блоха

Стани, в яких може знаходитись окремий кубіт, можна наочно демонструвати за допомогою сфери Блоха. Класичний біт на цій сфері може знаходитися лише на «північному полюсі» (стан $|0\rangle$ ) або на «південному полюсі» (стан $|1\rangle$ ). Решта поверхні сфери Блоха недоступна для класичного біта, але чистий стан кубіта може займати будь-яку точку сфери. Наприклад, чистий стан кубіта ${\frac {|0\rangle +i|1\rangle }{\sqrt {2}}}$ знаходитиметься на екваторі сфери, осі OY.

Поверхня сфери — це двовимірний простір, що представляє простір чистих станів кубіта. Цей простір має дві локальні ступені вільності. Інтуїтивно здавалося б, що простір повинен був мати чотири ступені вільності, оскільки $a$ і $b$ є комплексними й мають по дві ступені вільності. Однак, одна ступінь вільності зникає завдяки обмеженню $|a|^{2}+|b|^{2}=1$ . Іншу ступінь вільності, фазу кубіта, не можна виміряти, тож без обмеження загальності ми можемо обрати коефіцієнт $a$ дійсним, залишаючи тим самим дві ступені вільності.

Кубіт можна приготувати й у мішаному стані — статистичній суміші різних чистих станів. Мішані стани можна зобразити у вигляді точок всередині сфери Блоха.

Операції над чистими станами кубіта

Існують різні види фізичних операцій, які можна виконати над чистими станами кубіта.

Квантовий вентиль, який з точки зору математики являє собою унітарне перетворення кубіта. Унітарним перетворенням відповідають повороти вектора кубіта на сфері Блоха.
Вимірювання в стандартному базисі — операція, за допомогою якої отримується інформація про стан кубіта. Результатом буде стан $|0\rangle$ із ймовірністю $|a|^{2}$ або стан $|1\rangle$ із ймовірністю $|b|^{2}$ . Але операція вимірювання змінює значення a і b. Наприклад, якщо результатом був стан $|0\rangle$ , то a прийме значення 1 (відповідно до фази), а b — 0. Також слід зазначити, що вимірювання кубіта, заплутаного із іншою квантовою системою, перетворює чистий стан на мішаний.

Фізична реалізація

Будь-яка дворівнева квантова система може бути використана як кубіт. Також можна використовувати багаторівневі системи, якщо можливе відокремлення двох станів від решти (наприклад, основний та перший збуджений стани нелінійного осцилятора). Деякі з фізичних реалізацій кубіта, які у тій чи іншій мірі можна вважати дворівневою системою, були успішно втілені в життя. Як і звичайний комп'ютер, у якому використовуються класичні біти в різних втіленнях, наприклад, стан транзистора в процесорі, намагніченість поверхні жорсткого диску або наявність струму в дроті, гіпотетичний квантовий комп'ютер використовуватиме різноманітні реалізації кубітів.

Фізичне втілення	Назва	Носій інформації	$\|0\rangle$	$\|1\rangle$
Фотон	Поляризаційне кодування	Поляризація світла	Горизонтальна	Вертикальна
	Число фотонів	Стан Фока	Вакуумний стан	Стан із одним фотоном
	Часове кодування	Момент прибуття фотона	Раніше	Пізніше
Когерентний стан світла	Стиснуте світло	Квадратура	Амплітудно-стиснутий стан	Фазово-стиснутий стан
Електрони	Спін електрона	Спін	Вгору	Вниз
Електрони	Число електронів	Заряд	Немає електронів	Один електрон
Ядро	Ядерний спін (за допомоги ЯМР)	Спін	Вгору	Вниз
Оптичні ґратки	Атомний спін	Спін	Вгору	Вниз
Перехід Джозефсона	Надпровідний зарядовий кубіт	Заряд	Незаряджений надпровідний острівець (Q=0)	Заряджений надпровідний острівець (Q=2e, одна куперівська пара)
	Надпровідний потоковий кубіт	Струм	Струм за годинниковою стрілкою	Струм проти годинникової стрілки
	Надпровідний фазовий кубіт	Енергія	Основний стан	Перший збуджений стан
Пара квантових точок із одиничним зарядом	Локалізація електрона	Заряд	Електрон у лівій точці	Електрон у правій точці
Квантова точка	Спін квантової точки	Спін	Вниз	Вгору
Топологічна система з розривом	Неабелеві еніони	Коси збуджень	Залежить від топологічної системи	Залежить від топологічної системи
Гетероструктура Ван дер Ваальса[1]	Локалізація електрона	Заряд	Електрон у нижньому аркуші	Електрон у вирхньому аркуші

Див. також

Література

Вакарчук І. О. Квантова механіка. — 4-е видання, доповнене. — Л. : ЛНУ ім. Івана Франка, 2012. — 872 с.
Кайе Ф., Лафламм Р., Моска М. Введение в квантовые вычисления = An Introduction to Quantum Computing. — Ижевск : РХД, 2009. — 360 с.
Нильсен М., Чанг И. Квантовые вычисления и квантовая информация = Quantum Computation and Quantum Information. — М. : Мир, 2006. — 824 с.
Прескилл Дж. Квантовая информация и квантовые вычисления = Lecture Notes Ph219/CS219: Quantum Computation. — Ижевск : РХД, 2008-2011. — 464+312 с.

B. Lucatto (2019). Charge qubit in van der Waals heterostructures. Physical Review B 100 (12): 121406. Bibcode:2019PhRvB.100l1406L. arXiv:1904.10785. doi:10.1103/PhysRevB.100.121406. Проігноровано невідомий параметр |s2cid= (довідка)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] B. Lucatto (2019). Charge qubit in van der Waals heterostructures. Physical Review B 100 (12): 121406. Bibcode:2019PhRvB.100l1406L. arXiv:1904.10785. doi:10.1103/PhysRevB.100.121406. Проігноровано невідомий параметр |s2cid= (довідка)