Простір станів (теорія керування)

Структурна схема неперервної лінійної системи, описаної у вигляді змінних стану

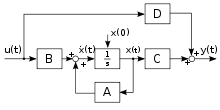
Для випадку лінійної системи з ${\displaystyle p}$ входами, ${\displaystyle q}$ виходами і ${\displaystyle n}$ змінними стану опис має вигляд:

${\displaystyle {\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}$

${\displaystyle \mathbf {y} (t)=C(t)\mathbf {x} (t)+D(t)\mathbf {u} (t)}$

де

${\displaystyle x(t)\in \mathbb {R} ^{n}}$ ; ${\displaystyle y(t)\in \mathbb {R} ^{q}}$ ; ${\displaystyle u(t)\in \mathbb {R} ^{p}}$ ;

${\displaystyle \operatorname {dim} [A(\cdot )]=n\times n}$, ${\displaystyle \operatorname {dim} [B(\cdot )]=n\times p}$, ${\displaystyle \operatorname {dim} [C(\cdot )]=q\times n}$, ${\displaystyle \operatorname {dim} [D(\cdot )]=q\times p}$, ${\displaystyle {\dot {\mathbf {x} }}(t):={d\mathbf {x} (t) \over dt}}$ :

${\displaystyle x(\cdot )}$ — вектор стану, елементи якого називають станами системи

${\displaystyle y(\cdot )}$ — вектор виходу,

${\displaystyle u(\cdot )}$ — вектор керування,

${\displaystyle A(\cdot )}$ — матриця системи,

${\displaystyle B(\cdot )}$ — матриця керування,

${\displaystyle C(\cdot )}$ — матриця виходу,

${\displaystyle D(\cdot )}$ — матриця прямого зв'язку.

Часто матриця ${\displaystyle D(\cdot )}$ є нульовою, це означає, що в системі немає явного прямого зв'язку .

Для дискретних систем запис рівнянь у просторі ґрунтується не на диференціальних, а на різницевих рівняннях:

${\displaystyle \mathbf {x} (nT+T)=A(nT)\mathbf {x} (nT)+B(nT)\mathbf {u} (nT)}$

${\displaystyle \mathbf {y} (nT)=C(nT)\mathbf {x} (nT)+D(nT)\mathbf {u} (nT)}$

Нелінійну динамічну систему n-го порядку можна описати у вигляді системи з n рівнянь 1-го порядку:

${\displaystyle {\dot {x}}_{1}=f_{1}(x_{1}(t);\ldots ,x_{n}(t),u_{1}(t),\ldots ,u_{m}(t))}$

${\displaystyle \vdots }$

${\displaystyle {\dot {x}}_{n}=f_{n}(x_{1}(t);\ldots ,x_{n}(t),u_{1}(t),\ldots ,u_{m}(t))}$

або в компактнішій формі:

${\displaystyle \mathbf {\dot {x}} (t)=\mathbf {f} (t,\mathbf {x} (t),\mathbf {u} (t))}$

${\displaystyle \mathbf {y} (t)=\mathbf {h} (t,\mathbf {x} (t),\mathbf {u} (t))}$.

Перше рівняння — це рівняння стану, друге — рівняння виходу.

У деяких випадках можлива лінеаризація опису динамічної системи для околу робочої точки ${\displaystyle (\mathbf {\tilde {x}} ,\mathbf {\tilde {u}} )}$ . У сталому режимі ${\displaystyle (\mathbf {\tilde {u}} =const)}$ для робочої точки ${\displaystyle \mathbf {\tilde {x}} =const,}$ справедливий такий вираз:

${\displaystyle \mathbf {\dot {x}} =\mathbf {f} (\mathbf {\tilde {x}} ,\mathbf {\tilde {u}} )=\mathbf {0} }$

Вводячи позначення:

${\displaystyle \delta \mathbf {u} =\mathbf {u} -\mathbf {\tilde {u}} }$

${\displaystyle \delta \mathbf {x} =\mathbf {x} -\mathbf {\tilde {x}} }$

Розклад рівняння стану ${\displaystyle \mathbf {f} (\mathbf {x} (t),\mathbf {u} (t))}$ в ряд Тейлора, обмежений першими двома членами дає такий вираз:

${\displaystyle \mathbf {f} (\mathbf {x} (t),\mathbf {u} (t))\approx \mathbf {f} (\mathbf {\tilde {x}} (t),\mathbf {\tilde {u}} (t))+{\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}\delta \mathbf {x} +{\frac {\delta \mathbf {f} }{\delta \mathbf {u} }}\delta \mathbf {u} }$

При взятті часткових похідних вектор-функції ${\displaystyle \mathbf {f} }$ за вектором змінних станів ${\displaystyle \mathbf {x} }$ і вектором вхідних впливів ${\displaystyle \mathbf {u} }$ виходять матриці Якобі відповідних систем функцій:

${\displaystyle {\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}={\begin{bmatrix}{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {x_{n}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {x_{n}} }}\end{bmatrix}}\quad {\frac {\delta \mathbf {f} }{\delta \mathbf {u} }}={\begin{bmatrix}{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {u_{p}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {u_{p}} }}\end{bmatrix}}}$ .

Аналогічно для функції виходу:

${\displaystyle {\frac {\delta \mathbf {h} }{\delta \mathbf {x} }}={\begin{bmatrix}{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {x_{n}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {x_{n}} }}\end{bmatrix}}\quad {\frac {\delta \mathbf {h} }{\delta \mathbf {u} }}={\begin{bmatrix}{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {u_{p}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {u_{p}} }}\end{bmatrix}}}$

З огляду на ${\displaystyle \delta \mathbf {\dot {x}} =\mathbf {\dot {x}} -\mathbf {\dot {\tilde {x}}} =\mathbf {\dot {x}} }$, лінеаризований опис динамічної системи в околі робочої точки набуде вигляду: де

${\displaystyle \mathbf {A} ={\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}\quad \mathbf {B} ={\frac {\delta \mathbf {f} }{\delta \mathbf {u} }}\quad \mathbf {C} ={\frac {\delta \mathbf {h} }{\delta \mathbf {x} }}\quad \mathbf {D} ={\frac {\delta \mathbf {h} }{\delta \mathbf {u} }}}$ .

Маятник є класичною вільною нелінійною системою. Математично рух маятника описує таке співвідношення:

${\displaystyle ml{\ddot {\theta }}(t)=-mg\sin \theta (t)-kl{\dot {\theta }}(t)}$

де

• ${\displaystyle \theta (t)}$ — кут відхилення маятника.
• ${\displaystyle m}$ — зведена маса маятника
• ${\displaystyle g}$ — прискорення вільного падіння
• ${\displaystyle k}$ — коефіцієнт тертя в підшипнику підвісу
• ${\displaystyle l}$ — довжина підвісу маятника

У такому випадку рівняння в просторі станів матимуть вигляд:

${\displaystyle {\dot {x_{1}}}(t)=x_{2}(t)}$

${\displaystyle {\dot {x_{2}}}(t)=-{\frac {g}{l}}\sin {x_{1}}(t)-{\frac {k}{m}}{x_{2}}(t)}$

де

• ${\displaystyle x_{1}(t):=\theta (t)}$ — кут відхилення маятника
• ${\displaystyle x_{2}(t):={\dot {x_{1}}}(t)}$ — кутова швидкість маятника
• ${\displaystyle {\dot {x_{2}}}(t):={\ddot {x_{1}}}(t)}$ — кутове прискорення маятника

Запис рівнянь стану в загальному вигляді:

${\displaystyle {\dot {\mathbf {x} }}(t)=\left({\begin{matrix}{\dot {x_{1}}}(t)\\{\dot {x_{2}}}(t)\end{matrix}}\right)=\mathbf {f} (t,x(t))=\left({\begin{matrix}x_{2}(t)\\-{\frac {g}{l}}\sin {x_{1}}(t)-{\frac {k}{m}}{x_{2}}(t)\end{matrix}}\right)}$ .

Лінеаризована матриця системи для моделі маятника в околі точки рівноваги ${\displaystyle \left({\tilde {x}}_{1}=0\right)}$ має вигляд:

${\displaystyle {\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}=\left({\begin{matrix}0&\ 1\\-{\frac {g}{l}}\cos {{\tilde {x}}_{1}}&\ -{\frac {k}{m}}\end{matrix}}\right)=\left({\begin{matrix}0&\ 1\\-{\frac {g}{l}}&\ -{\frac {k}{m}}\end{matrix}}\right)}$

За відсутності тертя в підвісі k = 0 отримаємо рівняння руху математичного маятника:

${\displaystyle {\ddot {x}}=-{\frac {g}{l}}x}$