Алгоритм гравітаційного пошуку

При розв'язуванні задач оптимізації з високою розмірністю простору пошуку, класичні алгоритми оптимізації не надають необхідне рішення, так як простір пошуку експоненціально зростає із складністю проблеми, тому рішення цих проблеми з використанням точних методів (наприклад, перебір) на практиці досить обмежене або інколи навіть неможливе.

Протягом останніх десятиліть спостерігається зростаючий інтерес до алгоритмів, які ґрунтуються на особливостях поведінки природних явищ. І ці алгоритми добре підходить для вирішення складних обчислювальних проблем, таких як оптимізація цільових функцій, розпізнавання образів, організація управління, обробка зображення, моделювання тощо. Тим не менше, немає конкретного алгоритму для досягнення найкращого розв'язку для всіх задач оптимізації. Деякі алгоритми дають краще рішення для деяких конкретних проблем, ніж інші. Таким чином, пошук нових евристичних алгоритмів оптимізації є відкритою проблемою.

У даній статті представлений новий алгоритм оптимізації на основі закону всесвітнього тяжіння, а саме Алгоритм Гравітаційного Пошук (англ. Gravitational Search Algorithm). Цей алгоритм заснований на законі гравітації Ньютона: «Кожна частка у Всесвіті притягує кожну іншу частку з силою, прямо пропорційною добутку їх мас і обернено пропорційною квадрату відстані між ними».

Слово «евристичний» з грецької означає «знати», «щоб знайти», «відкрити для себе». Евристичні алгоритми імітують фізичні або біологічні процеси. Найвідоміші алгоритми:

• Генетичний алгоритм
• Алгоритм імітації відпалу
• Алгоритм штучних імунних систем
• Мурашиний алгоритм
• Бджолиний алгоритм
• Алгоритм зозулі

Всі вищезазначені евристичні алгоритми мають стохастичну поведінку. Тим не менш, був запропонований детермінований алгоритм евристичного пошуку на основі законів гравітаційної кінематики, що називається «Центральна оптимізація сил». У деяких стохастичних алгоритмах пошук починається з однієї точки і продовжується в послідовному порядку, однак, у більшості евристичних алгоритмах виконується паралельний пошук з кількома початковими точками.

Можна виділити два аспекти евристичних алгоритмів на основі популяції: розвідка і використання. Розвідка полягає в можливості розширення простору пошуку, щоб знайти нові рішення. Щоб мати високу ефективність пошуку, потрібно знаходити компроміс між розвідкою та використанням. Для того, щоб уникнути попадання в локальний оптимум, алгоритм повинен використовувати результати розвідки протягом перших декількох ітерацій. Такі евристичні алгоритми використовують розвідку і використання, але вони використовують різні підходи. Іншими словами, всі пошукові алгоритми схожі. Використовуючи ці алгоритми пошуку можна отримати гарні результати, але немає евристичного алгоритму, який може забезпечити вищу продуктивність, у порівнянні з іншими, і забезпечити вирішення всіх проблем оптимізації.

Гравітація або тяжіння — властивість тіл із масою притягатись одне до одного. Гравітаційна взаємодія найслабша із фундаментальних взаємодій, однак її характерною особливістю є те, що тіла, які мають масу, завжди притягаються одне до одного. Притягання дуже великих мас в астрономічних масштабах створює значні сили, завдяки яким світ є таким, яким людина його знає.

Ньютонів закон всесвітнього тяжіння стверджує:

• Два тіла з масами m₁ та m₂ притягують одне одне із силою F прямо пропорційною добутку мас і обернено пропорційною квадрату відстані між ними:

${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}}$

Коефіцієнт пропорційності називається гравітаційною сталою. Її величина

${\displaystyle G=(6.6742\pm 0.0010)\cdot 10^{-11}}$ м³ кг⁻¹ с⁻²

У теоретичній фізиці розрізняють три види мас:

• Інертна маса — характеризує здатність тіла чинити опір зміні стану його руху під дією сили. За умови, що сила однакова, об'єкт з меншою масою легше змінює стан руху, ніж об'єкт з більшою масою.
• Активна гравітаційна — міра сили гравітаційного поля у зв'язку з конкретним об'єктом. Гравітаційне поле об'єкта з невеликою активною гравітаційна масою слабкіше, ніж об'єкта з більшою активної гравітаційної масою.
• Пасивна гравітаційна маса — міра сили взаємодії об'єкта з гравітаційним полем. В одному і тому ж гравітаційному полі, об'єкт з меншою пасивною гравітаційною масою відчуває меншу силу, ніж об'єкт з більшою пасивною гравітаційною масою.

У запропонованому алгоритмі, агенти розглядаються як об'єкти, і їх ефективність вимірюється їх масою. Всі ці об'єкти притягує один до одного сила тяжіння, і ця сила викликає глобальний рух усіх об'єктів до об'єктів з більшими масами. Таким чином, маси об'єктів наче співпрацюють, використовуючи гравітаційну силу як форму спілкування.

Важкі маси — відповідають гарним рішенням, вони рухаються повільніше, ніж інші, і це гарантує наявність пошукового кроку алгоритму. В Алгоритмі Гравітаційного пошуку, кожна маса (агент) має чотири характеристики:

• положення,
• інерційна маса,
• активна гравітаційна маса,
• пасивна гравітаційна маса.

Положення маси відповідає рішенню завдання, а гравітаційна та інерційна маси визначаються за допомогою оцінки-придатності.

Іншими словами, кожна маса — це рішення, і алгоритм вибирає напрямок пошуку рішення шляхом правильного налаштування гравітаційної і інерційної мас. З плином часу очікується, що буде знайдена найважча маса. Ця маса представить оптимальне рішення в просторі пошуку.

Алгоритм Гравітаційного пошуку можна розглядати як ізольовану систему мас. Це як маленький штучний світ мас, що підкоряється Закону Гравітації і Руху.

Точніше, маси повинні дотримуватися таких законів:

• Закон всесвітнього тяжіння: кожне тіло впливає на всі інші тіла і сила тяжіння між двома тілами безпосередньо пропорційна добутку їх мас і обернено пропорційна відстані між ними R. Ми використовуємо тут R замість R², оскільки згідно з результатами експериментів, R забезпечує кращі результати, ніж R², у всіх експериментальних випадках.
• Закон руху: швидкість руху будь-якої маси дорівнює сумі попередньої швидкості і зміни в швидкості. Зміна швидкості або прискорення будь-якої маси (тіла) в системі дорівнює результату ділення сили, що діяла на систему, на інерцію.

Тепер, розглянемо систему з N агентами (N мас). Визначимо положення i-го агента:
${\displaystyle X_{i}=(x_{i}^{1},...,x_{i}^{d},...,x_{i}^{n}),i=1,2...,N,\,}$
де ${\displaystyle x_{i}^{d}\,}$ представляє позицію i-го агента в d-й вимір.

У певний час t, ми визначимо силу, що діє на масу i від J маси так:
${\displaystyle F_{ij}^{d}(t)=G(t){\frac {M_{pi}(t)\times M_{aj}(t)}{R_{ij}(t)+\epsilon }}(x_{j}^{d}(t)-x_{i}^{d}(t)),\,}$ (1)

де ${\displaystyle M_{aj}}$ — активна гравітаційна маса, пов'язана з агентом j, ${\displaystyle M_{pi}}$ — пасивна гравітаційна маса, пов'язана з агентом i, ${\displaystyle G(t)}$ — гравітаційна стала в момент часу t, ${\displaystyle R_{ij}(t)}$ — евклідова відстань між двома агентами i і j:

${\displaystyle R_{ij}(t)=\parallel X_{i}(t),X_{j}(t)\parallel _{2}\,}$

Щоб увести стохастичну характеристику в алгоритм, ми припускаємо, що загальна сила, що діє на агент i з боку агента j — це випадково зважена сума d-x компонент сил, що діють з боку інших агентів:

${\displaystyle F_{i}^{d}(t)=\sum _{j=1,j\neq i}^{N}{rand_{j}F_{ij}^{d}(t)},\,}$

де rand_j це випадкове число в інтервалі [0, 1].

Отже, за законом руху, прискорення агента i в час t, та в напрямку ${\displaystyle a_{i}^{d}(t)}$, задається так:

${\displaystyle a_{i}^{d}(t)={\frac {F_{i}^{d}(t)}{M_{ii}(t)}},\,}$
де M_ii — маса i-го агента.

Крім того, наступна швидкість агента розглядається як сума поточної швидкості та прискорення. Тобто, положення і швидкість агента можна розрахувати так:

${\displaystyle v_{i}^{d}(t+1)=rand_{i}\times v_{i}^{d}(t)+a_{i}^{d}(t),\,}$

${\displaystyle x_{i}^{d}(t+1)=x_{i}^{d}(t)+v_{i}^{d}(t+1),\,}$

де rand_j це випадкове однорідне число в інтервалі [0, 1]. Ми використовуємо це випадкове число, щоб надати випадковості характеристикам пошуку.

Гравітаційна стала G, ініціалізується на початку і буде знижена з плином часу для того, щоб контролювати точність пошуку. Іншими словами, G є функцією від початкового значення (G₀) і часу (t):

${\displaystyle G(t)=G(G_{0},t).\,}$

Гравітаційна і інерційна маси просто обчислюється за оцінкою-придатності. Найважча маса означає, що агент ефективніший. Це означає, що кращі агенти мають більше тяжіння і рухаються повільно. Якщо припустити рівність гравітаційної та інерційної мас, то значення мас розраховуються з використанням карти придатності. Ми змінюємо гравітаційну і інерційну маси за наступними рівняннями:

${\displaystyle M_{ai}=M_{pi}=M_{ii}=M_{i},i=1,2,...,N,\,}$
${\displaystyle m_{i}(t)={\frac {fit_{i}(t)-worst(t)}{best(t)-worst(t)}},\,}$
${\displaystyle M_{i}(t)={\frac {m_{i}(t)}{\sum _{j=1}^{N}{m_{j}(t)}}},\,}$

Блок-схема алгоритму

де ${\displaystyle fit_{i}(t)\,}$ — представляють значення оцінки-придатності агента i в час t, а worst(t) та best(t) визначаються так (для задачі мінімізації):

${\displaystyle best(t)=\min _{j\epsilon [1,...,N]}{fit_{j}(t)},\,}$ (2)
${\displaystyle worst(t)=\max _{j\epsilon [1,...,N]}{fit_{j}(t)},\,}$ (3)

Слід зазначити, що для задачі максимізації, рівняння (2) і (3) замінюються рівняннями (4) і (5), відповідно:

${\displaystyle best(t)=\max _{j\epsilon [1,...,N]}{fit_{j}(t)},\,}$ (4)
${\displaystyle worst(t)=\min _{j\epsilon [1,...,N]}{fit_{j}(t)},\,}$ (5)

Один із способів хорошого компромісу між розвідкою і використанням є зниження числа агентів з використанням скінченного часу. Таким чином, пропонуємо розглядати тільки набір агентів з більшою масою та як вони впливають на інші. Тим не менш, треба буди обережним у використанні цієї стратегії, оскільки це може зменшити потужність розвідки та збільшити здібність використання.

Нагадаємо, що для того, щоб уникнути попадання в локальний оптимум алгоритм повинен використовувати розвідку на початку. За хибної ітерації, розвідка повинна зникати, а використання повинні поступово посилюватися. При підвищенні продуктивність алгоритму гравітаційного пошуку, за рахунок управління розвідкою і використанням тільки Kbest агенти будуть притягати інших. Kbest є функцією від часу, з початковим значенням K₀ на початку і зменшується з часом. Отже, на початку, всі агенти застосовують силу (впливають на інші тіла однаково), і з плином часу, Kbest зменшується лінійно, а в кінці буде тільки один агент, що впливає найбільше на інших. Таким чином, рівняння (1) може бути змінене так:

${\displaystyle F_{i}^{d}(t)=\sum _{j\epsilon Kbest,j\neq i}{rand_{j}F_{ij}^{d}(t)},\,}$ (6)
де Kbest — перші K агентів з найкращим співвідношенням оцінки-придатності і найбільшої маси.

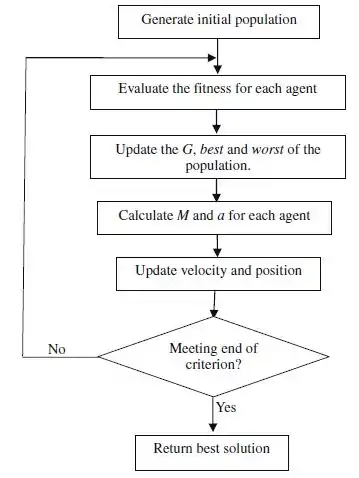
Отже, можна виділити наступні етапи запропонованого алгоритму:

1. Ідентифікація простору пошуку
2. Ініціалізації випадкових величин
3. Розрахунок загальної сили в різних напрямках
4. Коректування G(t), best(t), worst(t) та M_i(t),i=1,2,…,N
5. Розрахунок загального впливу сил в різних напрямках
6. Розрахунок швидкості і прискорення
7. Коректування (оновлення) позицій агентів
8. Повторити кроки з 3 по 7 доки не буде досягнуто критеріїв зупинки
9. Кінець

Щоб побачити, наскільки запропонований алгоритм є ефективним, слід розглянути наступні зауваження:

• Оскільки кожний агент може спостерігати за роботою інших, то сила тяжіння є інструментом для передачі інформації.
• Агент може бачити простір навколо себе, так як на нього діють сили сусідніх агентів.
• Важка маса має великий радіус дії тяжіння і, отже, більшу інтенсивність тяжіння. Таким чином, агенти з більш високою продуктивністю, мають більше гравітаційної маси. В результаті, агенти, як правило, рухаються в бік найкращого агента (найважчого агента).
• Інерція маси (тіла) протидіє руху, тому воно рухається повільно. Таким чином, важчі агенти рухаються повільніше і обшукують місце більш локально. Тому це можна розглядати як адаптивний курс навчання.
• Гравітаційна постійна регулює точності пошуку, тому з плином часу зменшується (за аналогією з температурою в алгоритмі імітації відпалу).
• Алгоритм Гравітаційного пошуку є алгоритмом з малим обсягом пам'яті. Тим не менш, він працює ефективно, як алгоритми з пам'яттю. Експериментальні результати показали гарну швидкість збіжності даного алгоритму.
• Ми припускаємо, що гравітаційна і інерційна маси однакові. Тим не менш, в деяких випадках можуть бути використані різні значення. Більша інерційна маса забезпечує повільніший рух агентів у просторі пошуку і, отже, точніший пошук. З іншого боку, велика гравітаційна маса викликає більше тяжіння між агентами, а це приводить до швидшої збіжності.

Порівняння з методом рою часток (Particle swarm optimization, PSO)

В основі методу — моделювання соціальної поведінки (зграї птахів). Цей оптимізаційний підхід змінює популяцію частинок (особин) шляхом застосування оператора відповідно до доречної інформації, отриманої з середовища. В результаті цього можна очікувати, що особина популяції буде рухатися в бік найкращого рішення. В методі рою часток ${\displaystyle x_{i}^{d}}$ та ${\displaystyle v_{i}^{d}}$ обчислюються так:

${\displaystyle x_{i}^{d}(t+1)=x_{i}^{d}(t)+v_{i}^{d}(t+1),\,}$

${\displaystyle v_{i}^{d}(t+1)=w(t)v_{i}^{d}(t)+c_{1}r_{i1}(pbest_{i}^{d}-x_{i}^{d}(t))+c_{2}r_{i2}(gbest^{d}-x_{i}^{d}(t)),\,}$ (7)

де r_i1 та r_i2 — дві випадкові величини в інтервалі [0,1], c₁ та c₂ — додатні константи, w — інерції. ${\displaystyle X_{i}=(x_{i}^{1},x_{i}^{2},...,x_{i}^{n})\,}$ та ${\displaystyle V_{i}=(v_{i}^{1},v_{i}^{2},...,v_{i}^{n})\,}$ представляють положення та швидкість й частки, відповідно. ${\displaystyle pbest_{i}=(pbest_{i}^{1},pbest_{i}^{2},...,pbest_{i}^{n})\,}$ та ${\displaystyle gbest=(gbest^{1},gbest^{2},...,gbest^{n})\,}$ представляють найкраще попереднє положення і-ї частки і її найкраще попереднє положення серед усіх частинок в популяції, відповідно.

З рівняння (7), отримуємо, що кожна частка намагається змінити своє положення (Х_і) використовуючи відстань між поточною позицією і pbest_i, а також відстань між поточною позицією і gbest.

В обох алгоритмах оптимізація виконується за рахунок руху агентів в просторі пошуку, проте стратегії руху різні. Деякі важливі відмінності полягають в наступному:

• В методі рою часток напрямок агента розраховується з використанням тільки двох найкращих позицій, pbesti і gbest. А в алгоритмі гравітаційного пошуку, напрямок агента розраховується на основі загальної сили отриманої від усіх інших агентів.
• В PSO, оновлення виконується без урахування якості рішень, а також значення оцінки-придатності не важливе в процедурі оновлення. В той час як в GSA сила пропорційна значенню оцінки-придатності, і тому агенти бачать простір пошуку навколо себе під впливом сили.
• В методі рою часток використовується багато пам'яті при оновленні значень pbest та gbest, а в алгоритмі гравітаційного пошуку важливе тільки поточне положення агента, тому для роботи алгоритму не треба багато пам'яті.
• В PSO, оновлення виконується без урахування відстані між рішеннями, у той час як в GSA сила обернено пропорційна відстані між рішеннями.
• І нарешті, відзначимо, що пошукові ідеї цих алгоритмів різні. PSO імітує соціальну поведінку птахів, а на створення GSA вплинули фізичні явища.

Хоча алгоритм гравітаційного пошуку ще досить новий у порівнянні з іншими методами, його вже використовують для вирішення багатьох прикладних задач. Зокрема алгоритм можна використовувати в таких задачах:

• за допомогою алгоритму пропонується визначити оптимальну конструкцію, склад посилених бетонних конструкції;
• для вирішення проблеми економічного врегулювання (англ. Economic Dispatch Problem);
• для вирішення проблеми пошуку найкоротшого шляху.

• Колективний інтелект
• Генетичний алгоритм
• Алгоритм імітації відпалу
• Мурашиний алгоритм
• Евристика
• Евристичний алгоритм
• Алгоритм зозулі

• Стаття «GSA: Алгоритм гравітаційного пошуку»^{[недоступне посилання з червня 2019]} (англ.)