Алгоритм художника

Назва «алгоритм художника» відноситься до техніки, яка використовується багатьма художниками живопису для віддалення частин сцени, які перекриваються частинами, розташованими ближче до спостерігача. Алгоритм художника сортує всі багатокутники в сцені по їх глибині і потім малює їх у порядку від найвіддаленішого до найближчого. Алгоритм буде зафарбувати ті частини, які зазвичай не видно — тим самим вирішуючи проблему видимості — ціною фарбування областей віддалених об'єктів, які не будуть видимими. Порядок, який використовує алгоритмом називається «порядок глибини», який використовує числову відстань до частин сцени: істотна властивість цього впорядкування, полягає в тому, якщо один об'єкт заступає частину іншого, тому перший об'єкт буде забарвлений після об'єкта, який він приховує. Таким чином, такий порядок може бути описаний як топологічне впорядкування орієнтованого ациклічного графу, що представляє розташування об'єктів[1].

Далекі гори пофарбовані першим, а потім більш близькі луги і дерева. Хоча деякі дерева далі від точки зору, ніж деяких частини лугів, упорядкування (гори, луки, дерева), оскільки незалежно від об'єкта впорядкування приховує будь-яку частину об'єкта який знаходиться пізніше.

Циклічне перекриття багатокутників — немає найближчого

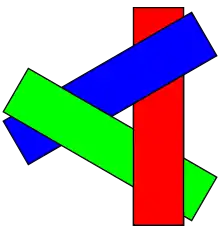
Алгоритм може не може розташувати об'єкти в деяких випадках. Зокрема при циклічному перекритті або обробці багатокутників. У разі циклічного перекриття, як показано на малюнку справа, багатокутники A, B, і C перекривають один одного таким чином, що неможливо визначити, який багатокутник найближчий. У цьому разі багатокутники повинні бути розрізані, для подальшого сортування. Алгоритм Невілла, запропонований в 1972, описує спосіб розрізання таких багатокутників. Багато таких способів є в обчислювальній геометрії.

Випадок «проколювання» багатокутників виникає тоді, коли один багатокутник перетинає площину іншого. Як і з циклічним перекриттям, ця проблема може бути вирішена за рахунок розрізання відповідного багатокутника.

В основних реалізаціях алгоритм живописця може бути не ефективним. Це змушує систему на надання кожній точці на кожному багатокутнику у видимій зоні, навіть якщо це багатокутник оклюзії в готовій сцені. Це означає, що для отримання докладних сцен, алгоритм живописця може бути податком комп'ютерного обладнання.

Зворотній алгоритм художника виводить впорядковані об'єкти починаючи з найближчого закінчуючи найвіддаленішим за правилом, що фарба не повинна бути застосована до тої частини зображення, яка вже пофарбована. При побудові зображення, це може бути дуже ефективним, оскільки відпадає потреба в розрахунку зображення (а для цього потрібен розрахунок освітлення, текстурування та інше) для частин більш віддалених від сцени, які закриті ближчими об'єктами. Однак у зворотнього алгоритму такі ж недоліки, як і у стандартного.

Ці та інші недоліки алгоритму призвели до розвитку методу Z-буфера, який можна розглядати як розвиток алгоритму художника, який попіксельно розв'язує питання глибини об'єкта. Навіть в таких системах, іноді використовується алгоритм художника. Так як реалізації Z-буфера звичайно використовують фіксовану точність регістрів буфера, яка реалізовано на апаратному рівні, тому можливі проблеми видимості через помилки округлення. Такі як дублювання або прогалини у з'єднанні між многокутниками. Щоб уникнути цього, деякі графічні реалізації «накладають» ребра таких многокутників, так само як і в алгоритмі художника. Це означає, що деякі пікселі будуть обчислені два рази (як і в алгоритмі художника), але це буде лише на невеликих ділянках зображення і незначно впливає на продуктивність всього алгоритму.

• Foley, James; van Dam, Andries; Feiner, Steven K.; Hughes, John F. (1990). en:Computer_Graphics:_Principles_and_Practice. Reading, MA, USA: Addison-Wesley. с. 1174. ISBN 0-201-12110-7.