Багаточастковий граф

k-частковий граф — граф, множину вершин якого можна розбити на k незалежних множин (часток). Еквівалентно, це граф, який можна розфарбувати за допомогою k кольорів так, що кінці будь-якого ребра будуть пофарбовані в різні кольори. При k = 2 k-частковий граф називається двочастковим[1].

Розпізнати двочастковий граф можна за поліноміальний час, але для будь-якого k > 2 задача визначення, чи є даний нерозфарбований граф k-частковим, стає NP-повною[2]. Втім, у деяких застосуваннях теорії графів k-частковий граф можна задати на вході вже розфарбованим; це може статися, коли множини вершин графу відповідають різним типам об'єктів. Наприклад, фолксономії математично моделювалися тричастковими графами, в яких три множини вершин відповідають користувачам системи, ресурсам, які позначаються тегами, і власне тегам[3]

Повний тричастковий граф K_2,2,2 — граф октаедра

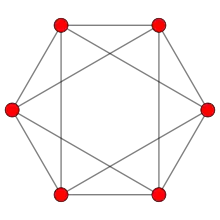
Повний k-частковий граф — це k-частковий граф, такий, що будь-які дві вершини, які належать до різних часток, суміжні[1]. Повний k-частковий граф можна описати нотацією

${\displaystyle K_{v_{1},v_{2},\ldots ,v_{k}},}$

де ${\displaystyle v_{1},v_{2},\ldots ,v_{k}}$ — число вершин у частках графу. Наприклад, ${\displaystyle K_{2,2,2}}$ — повний тричастковий граф правильного октаедра, що складається з трьох незалежних множин, кожна з яких включає дві протилежні вершини октаедра. Повний багаточастковий граф — це граф, який є повним k-частковим для деякого k[4].

Граф Турана — повний багаточастковий граф, потужності будь-яких двох часток якого відрізняються не більше ніж на 1. Повні багаточасткові графи — частковий випадок кографів.