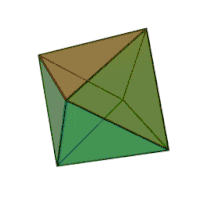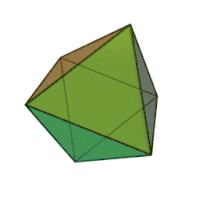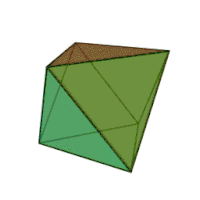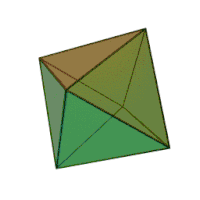
Октаедр
Октаедр (грец. οκτάεδρον, від грец. οκτώ, «вісім» і грец. έδρα — «основа») — многогранник з вісьма гранями. Правильний октаедр є одним з п'яти опуклих правильних многогранників[1], так званих платонових тіл; грані правильного октаедра — вісім правильних трикутників.
| Октаедр | |
|---|---|
 | |
| Тип | Правильний многогранник |
| Грань | трикутник |
| Граней | |
| Ребер | |
| Вершин | |
| Граней при вершині | |
| Тілесний кут при вершині |
ср |
| Точкова група симетрії |
Октаедрична (Oh) |
| Двоїстий многогранник | Куб |
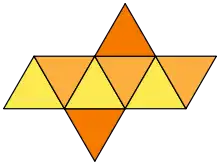
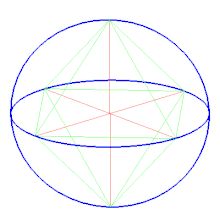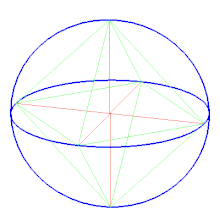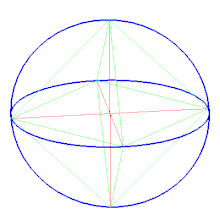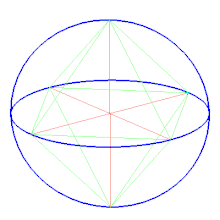

Правильний октаедр є двоїстим до куба. Він є повним усіканням тетраедра. Правильний октаедр є квадратною біпірамідою в кожному з трьох ортогональних напрямків. Він також є трикутною антипризмою в кожному з чотирьох напрямків.
Октаедр — тривимірний варіант більш загального поняття гіпероктаедр.
Правильний октаедр є тривимірною кулею в манхеттенській метриці.
Правильний октаедр
Правильний октаедр має 8 трикутних граней, 12 ребер, 6 вершин, в кожній його вершині сходяться 4 ребра.
Розміри
Якщо довжина ребра октаедра дорівнює а, то радіус сфери, описаної навколо октаедра (яка торкається всіх кутів), дорівнює:
радіус вписаної в октаедр сфери (яка торкається всіх граней) можна обчислити за формулою:
двогранний кут: , де .
Радіус напіввписаної сфери (яка торкається всіх ребер) дорівнює
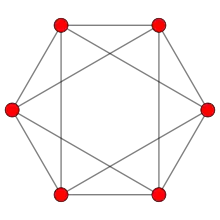
Ортогональні проєкції
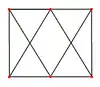
Октаедр має чотири спеціальні ортогональні проєкції, центровані ребром, вершиною, гранню і нормаллю до грані. Другий і третій випадок відповідають площинам Коксетера B2 і A2.
| Центровані | Ребром | Нормаллю до грані |
Вершиною | Гранню |
|---|---|---|---|---|
| Образ | 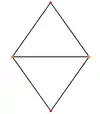 |
 |
 |
 |
| Проєктивна симетрія |
[2] | [2] | [4] | [6] |
Сферична мозаїка
Октаедр можна представити, як сферичну мозаїку і спроєктувати на площину за допомогою стереографічної проєкції. Ця проєкція конформна, зберігає кути, але не довжини і площу. Відрізки на сфері віддзеркалюються в дуги кіл на площині.
 |
 трикутно-центрована |
| Ортогональна проєкція | Стереографічна проєкція |
|---|
Декартові координати
Октаедр з довжиною ребра можна помістити в початок координат, так що його вершини лежатимуть на осях координат. Декартові координати вершин тоді будуть
- (±1, 0, 0);
- (0, ±1, 0);
- (0, 0, ±1).
У x-y-z прямокутній системі координат октаедр з центром з точці (a, b, c) і радіусом r — це множина всіх точок (x, y, z), таких, що
Площа і об'єм
Площа повної поверхні правильного октаедра з довжиною ребра a дорівнює
Об'єм октаедра (V) обчислюється за формулою:
Таким чином, об'єм октаедра в чотири рази більший за об'єм тетраедра з тією ж довжиною ребра, тоді як площа поверхні вдвічі більша (оскільки поверхня складається з 8 трикутників, а у тетраедра — з чотирьох).
Якщо октаедр розтягнути, щоб виконувалася рівність:
то формули для поверхні та об'єму перетворюються на:
Крім того, тензор моментів інерції розтягнутого октаедра дорівнюватиме:
Він зводиться до формули для правильного октаедра, коли:
Геометричні зв'язки
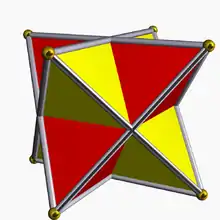
Внутрішня (спільна) частина конфігурації з двох тетраедрів є октаедром, а сама ця конфігурація називається зірчастим октаедром (лат.: stella octangula). Конфігурація є єдиною зірчастою формою октаедра. Відповідно, правильний октаедр є результатом відсікання від правильного тетраедра чотирьох правильних тетраедрів з половиною довжини ребра (тобто повного усікання тетраедра). Вершини октаедра лежать на серединах ребер тетраедра і октаедр пов'язаний з тетраедром так само, як кубооктаедр та ікосододекаедр пов'язані з іншими платоновими тілами. Можна розділити ребра октаедра у відношенні золотого перетину для визначення вершин ікосаедра. Для цього слід розташувати вектори на ребрах, так, щоб всі грані були оточені циклами. Потім ділимо кожне ребро в золотому відношенні вздовж векторів. Отримані точки є вершинами ікосаедра.
Октаедри і тетраедри можна чергувати, щоб побудувати однорідні відносно вершин, ребер і граней стільники, які Фуллер назвав октетною зв'язкою. Це єдина така мозаїка за винятком утвореної кубами, і вона є одним з 28 видів опуклих однорідних стільників.
Октаедр унікальний серед платонових тіл у тому, що тільки він має парне число граней при кожній вершині. Таким чином, це єдиний член групи, який має площини симетрії, що не перетинають жодну грань.
Якщо використовувати стандартну термінологію многогранників Джонсона, то октаедр можна назвати квадратною біпірамідою. Усікання двох протилежних вершин призводить до зрізаної біпіраміди.
Октаедр є 4-зв'язним. Це означає, що потрібно вилучити чотири вершини, щоб роз'єднати ті, що залишилися. Це один з чотирьох 4-зв'язних симпліціальних добре покритих многогранників, що означає, що всі найбільші незалежні множини вершин мають один і той самий розмір. Інші три многогранники з цією властивістю — п'ятикутна біпіраміда, плосконосий двоклиноїд і нерегулярний многогранник з 12 вершинами і 20 трикутними гранями[2].
- Октаедр можна вписати в тетраедр, при тому чотири з восьми граней октаедра будуть суміщені з чотирма гранями тетраедра, всі шість вершин октаедра будуть суміщені з центрами шести ребер тетраедра.
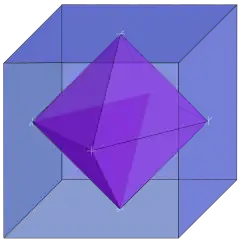
- Октаедр можна вписати в куб, при тому всі шість вершин октаедра будуть суміщені з центрами шести граней куба.
- В октаедр можна вписати куб, при тому всі вісім вершин куба будуть розташовані в центрах восьми граней октаедра.
Однорідне розфарбування і симетрія
Існує 3 однорідні розфарбовування октаедра, названі за їхніми кольорами граней: 1212, 1112, 1111.
Групою симетрії октаедра є Oh з порядком 48, тривимірна гіпероктаедральна група. У підгрупи цієї групи входять D3d (порядку 12), група симетрії трикутної антипризми, D4h (порядку 16), група симетрії квадратної біпіраміди, і Td (порядку 24), група симетрії повністю зрізаного тетраедра. Ці симетрії можна підкреслити шляхом різного розфарбовування граней.
| Назва | Октаедр | Повністю зрізаний тетраедр |
Трикутна антипризма | Квадратна біпіраміда | Ромбічна біпіраміда |
|---|---|---|---|---|---|
| Рисунок (Розфарбовування граней) |
 (1111) |
 (1212) |
 (1112) |
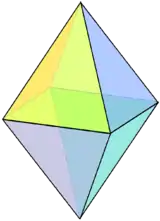 (1111) |
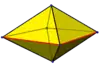 (1111) |
| Діаграма Коксетера | |||||
| Символ Шлефлі | {3,4} | r{3,3} | s{2,6} sr{2,3} |
ft{2,4} { } + {4} |
ftr{2,2} { } + { } + { } |
| Символ Візоффа | 4 | 3 2 | 2 | 4 3 | 2 | 6 2 | 2 3 2 | ||
| Симетрія | Oh, [4,3], (*432) | Td, [3,3], (*332) | D3d, [2+,6], (2*3) D3, [2,3]+, (322) |
D4h, [2,4], (*422) | D2h, [2,2], (*222) |
| Порядок | 48 | 24 | 12 6 |
16 | 8 |
Огранювання
Однорідний тетрагемігексаедр є огранюванням з тетраедральною симетрією правильного октаедра, який зберігає розташування ребер і вершин многогранника. Огранювання має чотири трикутні грані і 3 центральні квадрати.
 Октаедр |
 тетрагемігексаедр |
Неправильні октаедри
Такі многогранники комбінаторно еквівалентні правильному октаедру. Вони всі мають шість вершин, вісім трикутних граней і дванадцять ребер, що відповідає один до одного параметрам правильного октаедра.
- Трикутні антипризми — дві грані являють собою рівносторонні трикутники, що лежать у паралельних площинах і мають загальну вісь симетрії. Решта шість трикутників рівнобедрені.
- Чотирикутні біпіраміди, в яких щонайменше один екваторіальний чотирикутник лежить у площині. Правильний октаедр є спеціальним випадком, коли всі три чотирикутники є плоскими квадратами.
- Многогранник Шенгардта, неопуклий многогранник, який можна розбити на тетраедри без введення нових вершин.
Інші опуклі восьмигранники
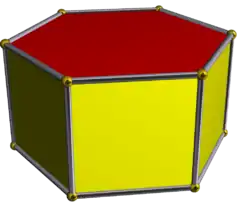
призма

тетраедр
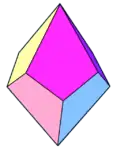
трапецоедр
У загальному випадку, октаедром можна назвати будь-який многогранник з вісьмома гранями. Правильний октаедр має 6 вершин і 12 ребер, мінімальна кількість для октаедра. Неправильні восьмигранники можуть мати до 12 вершин і 18 ребер[4]. Існує 257 топологічно різних опуклих восьмигранників, виключаючи дзеркальні копії. Зокрема, є 2, 11, 42, 74, 76, 38, 14 восьмигранників з числом вершин від 6 до 12 відповідно[5][6]. (Два многогранники «топологічно різні», якщо вони мають внутрішньо різне розташування граней і вершин, так що немає можливості перетворити одне тіло в інше просто зміною довжини ребер або кутів між ребрами або гранями.)
Деякі відомі неправильні восьмигранники:
- Шестикутна призма: Дві грані є паралельними правильними шестикутниками, шість квадратів з'єднують відповідні пари сторін шестикутників.
- Семикутна піраміда: Одна грань є семикутником (зазвичай правильним), а решта сім граней трикутниками (зазвичай рівнобедреними). Неможливо домогтися, щоб всі трикутні грані були рівносторонніми.
- Зрізаний тетраедр: Чотири грані тетраедра скорочуються до правильних шестикутників і утворюються три додаткові рівносторонні трикутні грані на місці відтятих вершин.
- Чотирикутний трапецоедр: Вісім граней конгруентні дельтоїдам.
Октаедри у фізичному світі
Октаедри в природі

- Багато природних кубічних кристалів мають форму октаедра. Це алмаз, сульфат алюмінію-калію, хлорид натрію, перовськіт, олівін, флюорит, шпінель.
- Форму октаедра мають міжатомні порожнини (пори) в щільноупакованих структурах чистих металів (нікелі, міді, магнії, титані, лантані та багатьох інших), а також іонних сполук (хлорид натрію, сфалерит, вюртцит та ін).
- Пластини сплаву камаситу в октаедритних метеоритах розташовані паралельно до восьми граней октаедра.
Октаедри в мистецтві і культурі

- В іграх гральна кісточка у вигляді октаедра відома як «d8».
- Якщо кожне ребро октаедра замінити одноомним резистором, то загальний опір між протилежними вершинами буде становити 1/2 ома, а між суміжними вершинами — 5/12 ома[7].
- Шість музичних нот можна розташувати на вершинах октаедра так, що кожне ребро є співзвучне секунді, а кожна грань — співзвучна терції.
Тетраедральна зв'язка
Каркас з повторюваних тетраедрів і октаедрів винайдений Фуллером в 1950-х роках і він відомий як просторова рама і вважається найміцнішою структурою, що чинить опір напругам консольної балки.
Пов'язані многогранники
Правильний октаедр можна збільшити до тетраедра додаванням чотирьох тетраедрів на грані, які чергуються. Додавання тетраедрів до всіх восьми граней утворює зірчастий октаедр.
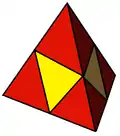 |
 |
| тетраедр | зірчастий октаедр |
|---|
Октаедр належить до родини однорідних многогранників, пов'язаних з кубом.
Шаблон:Октаедральні усікання
Він також є одним з найпростіших прикладів гіперсимплекса, многогранника, утвореного певним перетином гіперкуба з гіперплощиною.
Октаедр входить в послідовність многогранників з символом Шлефлі {3,n}, яка продовжується на гіперболічну площину.
Тетратетраедр
Правильний октаедр можна розглядати як повністю зрізаний тетраедр і можна назвати тетратетраедром. Це можна показати за допомогою розмальованої двома кольорами моделі. При цьому розфарбовуванні октаедр має тетраедральну симетрію.
Порівняння послідовності усікання тетраедра і його двоїстої фігури:
| Симетрія: [3,3], (*332) | [3,3]+, (332) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 | |||
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Двоїсті многогранники | |||||||
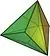 |
 |
 |
 |
 | |||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Вищенаведені тіла можна розуміти як зрізи, ортогональні до довгої діагоналі тесеракта. Якщо розташувати цю діагональ вертикально з висотою 1, то перші п'ять перерізів зверху на висотах r, 3/8, 1/2, 5/8 і s, де r — будь-яке число в інтервалі (0,1/4], а s — будь-яке число в інтервалі [3/4,1).
Октаедр як тетратетраедр існує в послідовності симетрій квазіправильних многогранників і мозаїк з конфігурацією вершин (3.n)2, проходячи від мозаїк на сфері до евклідової площини, а потім гіперболічної площини. У орбіфолдній нотації симетрії *n32 всі ці мозаїки є побудовами Візоффа всередині фундаментальної області симетрії з генерувальними точками на прямому куті області[8][9].
Шаблон:Квазірегулярні-3 мала таблиця
Трикутна антипризма
Як трикутної антипризмы октаедр пов'язаний з сімейством шестикутної диэдральной симетрії. Шаблон:Шестикутні діедральні усікання
Шаблон:Однорідні антипризми
Див. також
- Центроване октаедральне число
- Зірчастий октаедр
- Тріакісоктаедр
- Гекзакісоктаедр
- Зрізаний октаедр
- Координаційна теорія
- Октаедральна симетрія
- Граф октаедра
Примітки
- Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп. т.). — СПб., 1890—1907. (рос. дореф.)(рос.)
- Finbow, Hartnell, Nowakowski, Plummer, 2010, с. 894–912.
- Шаблон:MathWorld3(англ.)Шаблон:MathWorld3
- Steven Dutch. Enumeration of Polyhedra. Архів оригіналу за 10 жовтня 2011. Процитовано 27 жовтня 2017.
- Counting polyhedra
- Архівована копія. Архів оригіналу за 17 листопада 2014. Процитовано 27 жовтня 2017.
- Klein, 2002, с. 633–649.
- Williams, 1979.
- Two Dimensional symmetry Mutations by Daniel Huson
Література
- Большая советская энциклопедия
- Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski, Michael D. Plummer. On well-covered triangulations. III // Discrete Applied Mathematics. — 2010. — Т. 158, вип. 8. — DOI:.
- Douglas J. Klein. Resistance-Distance Sum Rules // Croatica Chemica Acta. — 2002. — Т. 75, вип. 2. Процитовано 2006-09-30.
- R. Williams. Chapter 5 The Kaleidoscope, Section: 5.7 Wythoff's // The Geometrical Foundation of Natural Structure: A Source Book of Design. — New York : Dover Publications, 1979.
Посилання
- Weisstein, Eric W. Octahedron(англ.) на сайті Wolfram MathWorld.
- Klitzing Polytopes, 3D convex uniform polyhedra
- Editable printable net of an octahedron with interactive 3D view
- Paper model of the octahedron
- K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Conway Notation for Polyhedra Try: dP4