Біполярна система координат

Біполярна система координат — ортогональна система координат на площині на основі кіл Аполлонія[1]. Криві, що відповідають сталим значенням змінних σ і τ перетинаються під прямими кутами. Координати задаються двома фокусами F₁ та F₂, зазвичай у точках (−a, 0) та (a, 0), відповідно, на осі іксів декартової системи координат.

Геометричний смисл біполярних координат. Кут σ утворений двома фокусами і точкою P, тоді як τ — логарифм відношення відстаней до фокусів. Відповідні кола сталих σ й τ показано червоним і синім, відповідно, вони перетинаються під прямими кутами (фіолетовий прямокутник).

Означення

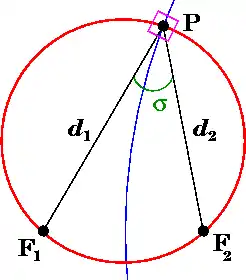
Зазвичай біполярні координати (σ, τ) визначають як:

x=a\ {\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}

y=a\ {\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}

де σ-координата точки P дорівнює куту $\angle$ F₁ P F₂, а τ-координата дорівнює натуральному логарифмові відношення відстаней d₁ та d₂ до фокусів

\tau =\ln {\frac {d_{1}}{d_{2}}}

( F₁ та F₂ розташовані в точках (−a, 0) і (a, 0), відповідно.) σ набирає значень від -π/2 до π/2, а τ — від $-\infty$ до $\infty$ . Можна записати,

x+iy=ai\cot \left({\frac {\sigma +i\tau }{2}}\right)

[2][3]

Криві сталих σ та τ

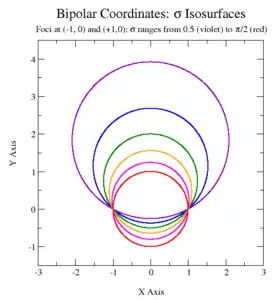
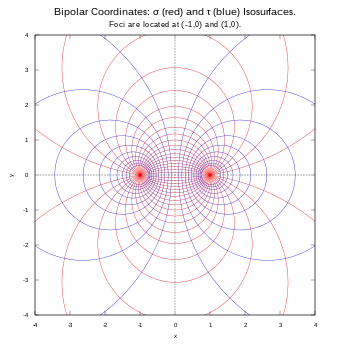
Криві сталих σ відповідають неконцентричним колам

x^{2}+\left(y-a\cot \sigma \right)^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}

що перетинаються в двох фокусах. Центри кіл сталих σ лежать на осі ігреків. Позитивні σ дають кола з центрами над віссю x, а негативні — нижче ві неї. Зі зростанням значення |σ| , радіус кола зменшується, а його центр наближається до початку координат (0, 0), досягаючи його при |σ| = π/2, що є максимальним значенням змінної.

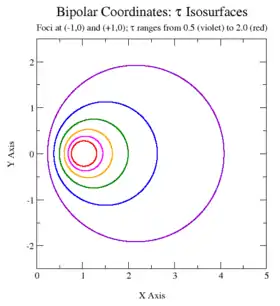
Криві сталих $\tau$ — кола різного радіусу, що не перетинаються між собою.

y^{2}+\left(x-a\coth \tau \right)^{2}={\frac {a^{2}}{\sinh ^{2}\tau }}.

Вони оточують фокуси, та не є концентричними. Центри кіл сталих τ лежать на осі іксів. Кола з дотатними τ лежать праворуч осі ігриків (x > 0), а кола з від'ємними τ лежать зліва від осі ігриків (x < 0). Крива τ = 0 відповідає осі ігриків (x = 0). Зі збільшенням абсолютньї величини τ радіус кіл зменшується, а їхні центри стягуються до фокусів.

Обернені співвідношення

Перейти від декартових до біполярних координат можна за наступними формулами:

\tau ={\frac {1}{2}}\ln {\frac {(x+a)^{2}+y^{2}}{(x-a)^{2}+y^{2}}}

та

\pi -\sigma =2\arctan {\frac {2ay}{a^{2}-x^{2}-y^{2}+{\sqrt {(a^{2}-x^{2}-y^{2})^{2}+4a^{2}y^{2}}}}}.

Існують дві чудові тотожності

\tanh \tau ={\frac {2ax}{x^{2}+y^{2}+a^{2}}}

та

\tan \sigma ={\frac {2ay}{x^{2}+y^{2}-a^{2}}}.

Коефіцієнти Ламе

Коефіцієнти Ламе для біполярних координат (σ, τ) дорівнюють:

h_{\sigma }=h_{\tau }={\frac {a}{\cosh \tau -\cos \sigma }}

Тож нескінченно малий елемент площі має форму

dA={\frac {a^{2}}{\left(\cosh \tau -\cos \sigma \right)^{2}}}\,d\sigma \,d\tau

а оператор Лапласа задається як:

\nabla ^{2}\Phi ={\frac {1}{a^{2}}}\left(\cosh \tau -\cos \sigma \right)^{2}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)

Інші диференціальні оператори, такі як $\nabla \cdot \mathbf {F}$ та $\nabla \times \mathbf {F}$ можна отримати в координатах (σ, τ), підставляючи коефіцієнти Ламе в загальні формули, виписані на сторінці ортогональна система координат.

Посилання на джерела

Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, Bipolar Coordinates, CD-ROM edition 1.0, May 20, 1999 Архівовано 12 грудня 2007 у Wayback Machine.
Polyanin, Andrei Dmitrievich (2002). Handbook of linear partial differential equations for engineers and scientists. CRC Press. с. 476. ISBN 1-58488-299-9.
Happel, John; Brenner, Howard (1983). Low Reynolds number hydrodynamics: with special applications to particulate media. Mechanics of fluids and transport processes 1. Springer. с. 497. ISBN 978-90-247-2877-0.

H. Bateman "Spheroidal and bipolar coordinates", Duke Mathematical Journal 4 (1938), no. 1, 39–50
Hazewinkel, Michiel, ред. (2001). Bipolar coordinates. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
Lockwood, E. H. "Bipolar Coordinates." Chapter 25 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 186–190, 1967.
Korn GA and Korn TM. (1961) Mathematical Handbook for Scientists and Engineers, McGraw-Hill.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[bip-1] Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, Bipolar Coordinates, CD-ROM edition 1.0, May 20, 1999 Архівовано 12 грудня 2007 у Wayback Machine.

[Polyanin-2] Polyanin, Andrei Dmitrievich (2002). Handbook of linear partial differential equations for engineers and scientists. CRC Press. с. 476. ISBN 1-58488-299-9.

[Happel-3] Happel, John; Brenner, Howard (1983). Low Reynolds number hydrodynamics: with special applications to particulate media. Mechanics of fluids and transport processes 1. Springer. с. 497. ISBN 978-90-247-2877-0.