Гармонійний пошук

Гармонійний пошук намагається знайти вектор, який оптимізує (мінімізує або максимізує) певну цільову функцію.

• Крок 1: Згенерувати випадкові вектори, стільки, скільки є місця у пам'яті гармонійного пошуку (hms), потім зберегти ці вектори у пам'яті гармонійного пошуку (hm).

${\displaystyle \mathbf {HM} ={\begin{bmatrix}x_{1}^{1}&\cdots &x_{n}^{1}&|&f(\mathbf {x} ^{1})\\\vdots &\ddots &\vdots &|&\vdots \\x_{1}^{hms}&\cdots &x_{n}^{hms}&|&f(\mathbf {x} ^{hms})\\\end{bmatrix}}.}$

• Крок 2: Згенерувати новий вектор ${\displaystyle \mathbf {x} '}$. Для кожної компоненти ${\displaystyle x_{i}^{'}}$,
  • з ймовірністю ${\displaystyle hmcr}$ (швидкість вибору значення з пам'яті гармонійного пошуку;0 ≤ ${\displaystyle hmcr}$ ≤ 1), вибрати збережене значення з hm ${\displaystyle x_{i}^{'}\leftarrow x_{i}^{int(u(0,1)*hms)+1}}$
  • з ймовірністю ${\displaystyle 1-hmcr}$, вибрати випадкове значення в межах допустимого діапазону.
• Крок 3: Виконання додаткових робіт, якщо значення в кроці 2 прийшло від hm.
  • з ймовірністю ${\displaystyle par}$ (крок регулювання швидкості; 0 ≤ ${\displaystyle par}$ ≤ 1), змінити ${\displaystyle x_{i}^{'}}$ на малу величину: ${\displaystyle x_{i}^{'}\leftarrow x_{i}^{'}+\delta }$ чи ${\displaystyle x_{i}^{'}\leftarrow x_{i}^{'}-\delta }$ для дискретного значення; чи ${\displaystyle x_{i}^{'}\leftarrow x_{i}^{'}+fw\cdot u(-1,1)}$ для безперервної змінної.
  • з ймовірністю ${\displaystyle 1-par}$, нічого не робити.
• Крок 4: Якщо ${\displaystyle \mathbf {x} ^{'}}$ краще, ніж найгірший вектор ${\displaystyle \mathbf {x} ^{Worst}}$ у hm, замінити ${\displaystyle \mathbf {x} ^{Worst}}$ на ${\displaystyle \mathbf {x} '}$.
• Крок 5: Повторення з кроку 2 до кроку 4, поки критерій не буде виконано

Параметри алгоритму:

• ${\displaystyle hms}$ : Розмір пам'яті гармонійного пошуку. Як правило, варіюється від 1 до 100 . (Стандартне значення = 30)
• ${\displaystyle hmcr}$ : Швидкість вибору значення з пам'яті гармонійного пошуку. Як правило, варіюється від 0,7 до 0,99. (Стандартне значення = 0,9)
• ${\displaystyle par}$ : Швидкість вибору сусідніх значень. Як правило, варіюється від 0,1 до 0,5. (Стандартне значення = 0,3)
• ${\displaystyle \delta }$ : Обсяг між двома сусідніми значеннями в дискретному наборі кандидатів.
• ${\displaystyle fw}$ (пропускна здатність) : Сума максимальної зміни кроку настройки. Це може бути (0,01 × допустимого діапазону) до (0,001 × допустимого діапазону).

Пазл судоку у процесі розв'язання

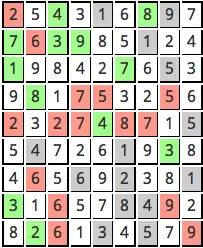
Одне із застосувань алгоритму гармонійного пошуку може бути розв'язання судоку.

Для початку з'ясуємо які ноти є у гармонії і, потім, вирахуємо якість рішення. Перш за все, зверніть увагу, що для будь-якого рішення, яке буде розглядатися як таке, кожна клітина повинна мати значення. Деякі значення задаються головоломкою, а деякі повинні бути вирішені нами. Ми прагнемо знайти значення для кожної комірки, таке що немає жодних конфліктів, або, іншими словами, оптимальним вирішенням цієї проблеми є судоку, яка має всі комірки заповнені не порушуючи правила гри. Ми моделюємо вартість кожної з невідомих комірок як одну ноту в гармонії, зі значенням ноти яке є цілим числом від 1 до 9. Справа приклад вирішення судоку за допомогою алгоритму гармонійного пошуку. На картинці наведено приклад рішення, запропоновані в ранній ітерації пошуку гармонії.

• Зелені комірки не порушують правила
• Червоні комірки клітин порушують або рядок або стовпець
• Білі комірки були дані головоломкою
• Сірі комірки мають тільки одне значення при даному розташуванні зелених та красних комірок

Зелені, сірі та червоні комірки представляють вибір для невідомих комірок.

Далі, ми вирішуємо, як оцінити якість даного рішення. Найочевидніший спосіб для оцінення алгоритму є наступним: підрахувати тільки кількість порушень в головоломці (підрахувати кількість червоних комірок). Оптимальне вирішення це глобальний мінімум функції Q, де ${\displaystyle Q=\sum _{i}^{9}\sum _{j}^{9}{S_{i},_{j}-45}+\sum _{j}^{9}\sum _{i}^{9}{S_{i},_{j}-45}+\sum _{k}^{9}\sum _{_{(}i,j)inB^{k}}{S_{i},_{j}-45},\,}$

де ${\displaystyle S_{i},_{j}}$ — комірка, де ${\displaystyle i}$ — кількість комірок враховуючи зліва, ${\displaystyle j}$ — згори, ${\displaystyle B_{k}}$ — усі клітини у k-му блоці.

Вища евристична функція дає нам детальнішу міру вирішення оптимального рішення. Вона працює наступним чином: бере суму кожного ряду і віднімає 45, що являє собою суму чисел від 1 до 9. Якщо певний ряд складається з двох 1 замість 1 і 2, сума чисел у рядку не буде 45, і Q не буде мінімальним. Правильне рішення для судоку матиме Q = 0. Важливо бачити, що сума рядків може бути 45, хоча номери в ньому, точно не встановлені ​​від 1 до 9. Наприклад, може статися наступне сума {1,2,2,5,5,6,7,8,9} = 45. Однак, якщо цей випадок має місце в одному рядку, то сума для стовпців, що проходять через ряд, або суму на один з блоків, що містять рядки не буде 45, рухаючи остаточне значення Q від 0, отже, це позначає субоптимальну якість відповідно до наших побажань. Єдиний спосіб щоб отримати в рядку, стовпці і блоці суму 45 — це єдиний варіант мати 1 — 9 в кожному контейнері. Таким чином, ноти для гармонії це множина значень невідомих комірок, а якість гармонії це оцінка функції Q в згенерованому судоку. За допомогою цих двох рішень, ми можемо тепер використовувати гармонійний пошук, щоб знайти рішення (якщо воно існує) до даної судоку.

Алгоритм Гармонійного пошуку застосовується до багатьох оптимізаційних проблем, таких як:

Застосування у реальному світі:

• Оптимальне рішення судоку
• Планування оптимального розкладу
• Логістичні проблеми

У Інформатиці:

• Класторування веб сторінки
• Узагальнення тексту
• Робототехніка

У електронній інженерії:

• Системи диспетчеризації
• Фотоелектронне виявлення
• Проектування системи живлення
• Проектування системи мобільного зв'язку

Гармонійний пошук може застосовуватися в:

• Еволюційному моделюванні
• Метаалгоритмах
• Стохастичній оптимізації
• Оптимізація (математика)

У еволюційних методах:

• Еволюційний алгоритм, включаючи:
  • Генетичні алгоритми
• алгоритми Колективного інтелекту, включаючи:
  • Мурашиний алгоритм
  • Метод рою часток

У метаалгоритмах, включаючи:

• Алгоритм імітації відпалу

• Еволюційний алгоритм
• Колективний інтелект

• Реалізація алгоритму на CoffeeScript(JavaScript)-http://harry.me/2011/05/07/neat-algorithms---harmony-search/
• Реалізація алгоритму на C# — https://sites.google.com/site/fesangharyweb/downloads
• Реалізація алгоритму на С++ — https://sites.google.com/site/multiobjectivehs/