Метод рою часток

Метод рою часток, МРЧ (англ. Particle Swarm Optimization, PSO) — метод чисельної оптимізації, для використання якого не потрібно знати точного градієнта оптимізованої функції. МРЧ був доведений Кеннеді, Еберхартом і Ші[1][2] і спочатку призначався для імітації соціальної поведінки. Алгоритм був спрощений, і було зауважено, що він придатний для виконання оптимізації. Книга Кеннеді й Еберхарта[3] описує багато філософських аспектів МРЧ і так званого ройового інтелекту. Велике дослідження застосувань МРЧ зроблене Полі[4][5]. МРЧ оптимізує функцію, підтримуючи популяцію можливих розв'язків, називаних частками, і переміщаючи ці частки в просторі розв'язків згідно із простою формулою. Переміщення підпорядковуються принципу найкращого знайденого в цьому просторі положення, що постійно змінюється при знаходженні частками вигідніших положень.

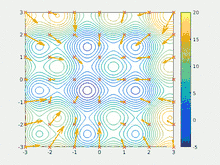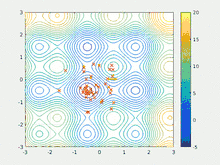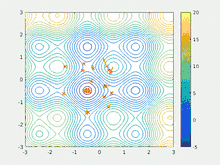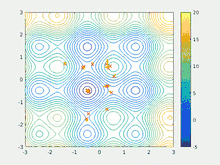
Рій часток, що шукає глобальний мінімум функції

Алгоритм

Нехай f: ℝⁿ →ℝ — цільова функція, яку потрібно мінімізувати, S — кількість часток у рою, кожній з яких зіставлена координата x_i ∈ ℝⁿ у просторі рішень і швидкість v_i ∈ ℝⁿ. Нехай також p_i — найкраще з відомих положень частки i, а g — найкращий відомий стан рою в цілому. Тоді загальний вигляд методу рою часток такий.

Для кожної частки i = 1, …, S зробити:
- Згенерувати початкове положення частки за допомогою випадкового вектора x_i ~ U(b_lo, b_up), що має багатовимірний рівномірний розподіл. b_lo і b_up — нижня й верхня границі простору рішень відповідно.
- Присвоїти найкращому відомому положенню частки його початкове значення: p_i ← x_i.
- Якщо (f(p_i) < f(g)), то оновити найкращий відомий стан рою: g ← p_i.
- Присвоїти значення швидкості частки: v_i ~ U(-(b_up-b_lo), (b_up-b_lo)).
Поки не виконаний критерій зупинки (наприклад, досягнення заданого числа ітерацій або необхідного значення цільової функції), повторювати:
- Для кожної частки i = 1, …, S зробити:
  - Згенерувати випадкові вектори r_p, r_g ~ U(0,1).
  - Оновити швидкість частки: v_i ← ω v_i + φ_p r_p × (p_i-x_i) + φ_g r_g × ( g-x_i), де операція × означає покомпонентне множення.
  - Оновити положення частки переносом x_i на вектор швидкості: x_i ← x_i + v_i. Зауважимо, що цей крок виконується незалежно від поліпшення значення цільової функції.
  - Якщо (f(x_i) < f(p_i)), то робити:
    - Оновити найкраще відоме положення частки: p_i ← x_i.
    - Якщо (f(p_i) < f(g)), то оновити найкращий відомий стан рою в цілому: g ← p_i.
Тепер g містить найкраще зі знайдених рішень.

Параметри ω, φ_p, і φ_g вибираються обчислювачем і визначають поведінку й ефективність методу в цілому. Ці параметри є предметом багатьох досліджень (див. нижче).

Підбір параметрів

Вибір оптимальних параметрів методу рою часток — тема значної кількості дослідницьких робіт, див., наприклад, роботи Ші й Еберхарта[6][7], Карлісла й Дозера[8], ван ден Берга[9], Клерка й Кеннеді[10], Трелеа[11], Браттона й Блеквела[12], а також Еверса[13].

Простий і ефективний шлях добору параметрів методу запропонований Педерсеном й іншими авторами[14][15]. Вони ж провели чисельні експерименти з різними оптимізаційними задачами й параметрами. Техніка вибору цих параметрів називається мета-оптимізацією, тому що інший оптимізаційний алгоритм використовується для «налаштовування» параметрів МРЧ. Вхідні параметри МРЧ із найкращою продуктивністю виявилися суперечним основним принципам, описаним у літературі, і часто дають задовільні результати оптимізації для простих випадків МРЧ. Реалізацію їх можна знайти у відкритій бібліотеці SwarmOps.

Варіанти алгоритму

Постійно пропонуються нові варіанти алгоритму рою часток для поліпшення продуктивності методу. Існує кілька тенденцій у цих дослідженнях, одна з яких пропонує створити гібридний оптимізаційний метод, що використовує МРЧ у комбінації з іншими алгоритмами, див. наприклад[16][17]. Інша тенденція пропонує яким-небудь чином прискорити роботу методу, наприклад, відходом назад або зміною порядку руху часток (про це див.[18][19][13]). Також є спроби адаптувати поведінкові параметри МРЧ у процесі оптимізації[20].

Див. також

Примітки

Kennedy J., Eberhart R. (1995). Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks IV. с. 1942–1948.
Shi Y., Eberhart R.C. (1998). A modified particle swarm optimizer. Proceedings of IEEE International Conference on Evolutionary Computation. с. 69–73.
Kennedy J., Eberhart R.C. (2001). Swarm Intelligence. Morgan Kaufmann. ISBN 1-55860-595-9.
Poli R. An analysis of publications on particle swarm optimisation applications // Technical Report CSM-469. — Department of Computer Science, University of Essex, UK, 2007.
Poli, R. (2008). Analysis of the publications on the applications of particle swarm optimisation. Journal of Artificial Evolution and Applications: 1–10. doi:10.1155/2008/685175.
Shi Y., Eberhart R.C. (1998). Parameter selection in particle swarm optimization. Proceedings of Evolutionary Programming VII (EP98). с. 591–600.
Eberhart R.C., Shi Y. (2000). Comparing inertia weights and constriction factors in particle swarm optimization. Proceedings of the Congress on Evolutionary Computation 1. с. 84–88.
Carlisle A., Dozier G. (2001). An Off-The-Shelf PSO. Proceedings of the Particle Swarm Optimization Workshop. с. 1–6.
Van den Bergh, F. (2001). An Analysis of Particle Swarm Optimizers (PhD thesis). University of Pretoria, Faculty of Natural and Agricultural Science.
Clerc M., Kennedy J. (2002). The particle swarm - explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation 6 (1): 58–73.
Trelea, I.C. (2003). The Particle Swarm Optimization Algorithm: convergence analysis and parameter selection. Information Processing Letters 85: 317–325.
Bratton D., Blackwell T. (2008). A Simplified Recombinant PSO. Journal of Artificial Evolution and Applications.
Evers, G. (2009). An Automatic Regrouping Mechanism to Deal with Stagnation in Particle Swarm Optimization (Master's thesis). The University of Texas - Pan American, Department of Electrical Engineering.
Pedersen, M.E.H. (2010). Tuning & Simplifying Heuristical Optimization (PhD thesis). University of Southampton, School of Engineering Sciences, Computational Engineering and Design Group.
Pedersen, M.E.H.; Chipperfield, A.J. (2010). Simplifying particle swarm optimization. Applied Soft Computing 10: 618–628.
Lovbjerg M., Krink T. (2002). The LifeCycle Model: combining particle swarm optimisation, genetic algorithms and hillclimbers. Proceedings of Parallel Problem Solving from Nature VII (PPSN). с. 621–630.
Niknam T., Amiri B. (2010). An efficient hybrid approach based on PSO, ACO and k-means for cluster analysis. Applied Soft Computing 10 (1): 183–197.
Lovbjerg M., Krink T. (2002). Extending Particle Swarm Optimisers with Self-Organized Criticality. Proceedings of the Fourth Congress on Evolutionary Computation (CEC) 2. с. 1588–1593.
Xinchao, Z. (2010). A perturbed particle swarm algorithm for numerical optimization. Applied Soft Computing 10 (1): 119–124.
Zhan Z-H., Zhang J., Li Y., Chung H.S-H. (2009). Adaptive Particle Swarm Optimization. IEEE Transactions on Systems, Man, and Cybernetics 39 (6): 1362–1381.

Посилання

Particle Swarm Central. Новини, люди, місця, програми, статті й ін. Зокрема, див. поточний стандарт МРЧ. (англ.)
SwarmOps. Підбор параметрів / калібрування МРЧ і інші мета-оптимізаційні методи. Програмна бібліотека на мовах C і C#.
EvA2 — комплексний інструмент еволюційних методів оптимізації й МРЧ із відкритим вихідним кодом, написаний на Java.
ParadisEO потужний C++ фреймворк, призначений для створення різних метаевристик, включаючи алгоритми МРЧ. Готові до використання алгоритми, багато підручників, що допомагають швидко створити власний варіант МРЧ.
Код МРЧ на FORTRAN Вимірювання продуктивності на тестових функціях.
JSwarm-PSO Пакет МРЧ-оптимізації
Модуль МРЧ на Perl
Модуль МРЧ на Lua
Java-аплет для 3D-візуалізації МРЧ
Java-аплет для 3D-візуалізації МРЧ із вихідним кодом
Посилання на вихідні коди алгоритмів МРЧ
CILib — GPLed computational intelligence simulation and research environment written in Java, includes various PSO implementations
МРЧ-модуль для MATLAB
Використання реалізації МРЧ на Python для розв'язання головоломки про перетинання сходів.
МРЧ-проект на Scheme
Простий приклад МРЧ на Haskell
ECF — Evolutionary Computation Framework різні алгоритми, генотипи, розпаралелювання, підручники.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[kennedy95particle-1] Kennedy J., Eberhart R. (1995). Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks IV. с. 1942–1948.

[shi98modified-2] Shi Y., Eberhart R.C. (1998). A modified particle swarm optimizer. Proceedings of IEEE International Conference on Evolutionary Computation. с. 69–73.

[kennedy01swarm-3] Kennedy J., Eberhart R.C. (2001). Swarm Intelligence. Morgan Kaufmann. ISBN 1-55860-595-9.

[poli07analysis-4] Poli R. An analysis of publications on particle swarm optimisation applications // Technical Report CSM-469. — Department of Computer Science, University of Essex, UK, 2007.

[poli08analysis-5] Poli, R. (2008). Analysis of the publications on the applications of particle swarm optimisation. Journal of Artificial Evolution and Applications: 1–10. doi:10.1155/2008/685175.

[shi98parameter-6] Shi Y., Eberhart R.C. (1998). Parameter selection in particle swarm optimization. Proceedings of Evolutionary Programming VII (EP98). с. 591–600.

[eberhart00comparing-7] Eberhart R.C., Shi Y. (2000). Comparing inertia weights and constriction factors in particle swarm optimization. Proceedings of the Congress on Evolutionary Computation 1. с. 84–88.

[carlisle01offtheshelf-8] Carlisle A., Dozier G. (2001). An Off-The-Shelf PSO. Proceedings of the Particle Swarm Optimization Workshop. с. 1–6.

[bergh01thesis-9] Van den Bergh, F. (2001). An Analysis of Particle Swarm Optimizers (PhD thesis). University of Pretoria, Faculty of Natural and Agricultural Science.

[clerc02explosion-10] Clerc M., Kennedy J. (2002). The particle swarm - explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation 6 (1): 58–73.

[trelea03particle-11] Trelea, I.C. (2003). The Particle Swarm Optimization Algorithm: convergence analysis and parameter selection. Information Processing Letters 85: 317–325.

[bratton08simplified-12] Bratton D., Blackwell T. (2008). A Simplified Recombinant PSO. Journal of Artificial Evolution and Applications.

[evers09thesis-13] Evers, G. (2009). An Automatic Regrouping Mechanism to Deal with Stagnation in Particle Swarm Optimization (Master's thesis). The University of Texas - Pan American, Department of Electrical Engineering.

[pedersen08thesis-14] Pedersen, M.E.H. (2010). Tuning & Simplifying Heuristical Optimization (PhD thesis). University of Southampton, School of Engineering Sciences, Computational Engineering and Design Group.

[pedersen08simplifying-15] Pedersen, M.E.H.; Chipperfield, A.J. (2010). Simplifying particle swarm optimization. Applied Soft Computing 10: 618–628.

[lovbjerg02lifecycle-16] Lovbjerg M., Krink T. (2002). The LifeCycle Model: combining particle swarm optimisation, genetic algorithms and hillclimbers. Proceedings of Parallel Problem Solving from Nature VII (PPSN). с. 621–630.

[niknam10efficient-17] Niknam T., Amiri B. (2010). An efficient hybrid approach based on PSO, ACO and k-means for cluster analysis. Applied Soft Computing 10 (1): 183–197.

[lovbjerg02extending-18] Lovbjerg M., Krink T. (2002). Extending Particle Swarm Optimisers with Self-Organized Criticality. Proceedings of the Fourth Congress on Evolutionary Computation (CEC) 2. с. 1588–1593.

[xinchao10perturbed-19] Xinchao, Z. (2010). A perturbed particle swarm algorithm for numerical optimization. Applied Soft Computing 10 (1): 119–124.

[zhan09adaptive-20] Zhan Z-H., Zhang J., Li Y., Chung H.S-H. (2009). Adaptive Particle Swarm Optimization. IEEE Transactions on Systems, Man, and Cybernetics 39 (6): 1362–1381.