Граф Хортона
У математичної області теорії графів, граф Хортона або 96-граф Хортона являє собою 3-регулярний граф з 96 вершинами і 144 реберами, виявлених Джохефом Хортоном. Опубліковано Бонді і Мурті в 1976 році, вона забезпечує контрприклад до гіпотези Татта, що кожен кубічний 3-зв'язний двочастковий граф є гамільтоновим графом.[1][2]
| Граф Хортон | |
|---|---|
 | |
| Названий на честь | Джозефа Хортона |
| Вершин | 96 |
| Ребер | 144 |
| Радіус | 10 |
| Діаметр | 10 |
| Обхват | 6 |
| Автоморфізм |
96 (Z/2Z×Z/2Z×S4) |
| Хроматичне число | 2 |
| Хроматичний індекс | 3 |
| Властивості | Кубічний Двороздільний |
Після графу Хортона, були знайдені кілька невеликих контрприкладів до гіпотези Татта. Серед них 92 вершин графу по Хортону, опубліковані в 1982 році, 78 вершин графу по Овенсу опублікований в 1983 році й два графу Єгингхема-Хортона (54 і 78 вершин). [3][4]
Перший граф Єгингхема — Хортона був опублікований в 1981 році і був близько 78. В той час це була найменший контрприклад до гіпотези Татта. Другий був опублікований Єгингхемем і Хортоном в 1983 році і був близько 54. Чи є менше негамільтонів кубічний 3-зв'язний двочастковий граф на даний час невідомо.
У негамільтонова кубічного графу з великою кількістю довгих циклів, граф Хортона забезпечує хороший орієнтир для програм, які виконують пошук гамільтонових циклів.[5]
Графік Хортон має хроматичний номер 2,хроматичний індекс 3, радіус 10, діаметр 10 і обхват 6. Це також реберно 3-зв'язний граф.
Група автоморфізмів графу Хортона має порядок 96 і ізоморфна з/2з×з/2з×з4, прямий добуток чверті групи Клейна і симетрична група S4.
Характеристичний многочлен графу Хортон:
.
Галерея
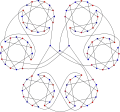 У хроматичному числі з Хортон графік 2.
У хроматичному числі з Хортон графік 2. Хроматичне число графу Хортона 2.
Хроматичне число графу Хортона 2. Элингхем-Хортон 54-граф, менший контрприклад до гіпотези Татта.
Элингхем-Хортон 54-граф, менший контрприклад до гіпотези Татта.
Посилання
- Tutte, W. T. «On the 2-Factors of Bicubic Graphs.»
- Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications.
- Horton, J. D. «On Two-Factors of Bipartite Regular Graphs.»
- Owens, P. J. «Bipartite Cubic Graphs and a Shortness Exponent.»
- V. Ejov, N. Pugacheva, S. Rossomakhine, P. Zograf «An effective algorithm for the enumeration of edge colorings and Hamiltonian cycles in cubic graphs» arXiv:math/0610779v1.