Двозв'язний граф
У теорії графів двозв'язний граф — це зв'язний і неподільний граф, в тому сенсі, що видалення будь-якої вершини не призведе до втрати зв'язності. Таким чином, двозв'язний граф не має шарнірів.
Властивість вершинної 2-зв'язності еквівалентна двозв'язності графу з одним винятком — повний граф з двома вершинами іноді вважається двозв'язним, але не вершинно-двозв'язним.
Ця властивість особливо корисна при розгляді графів з подвійним резервуванням, щоб уникнути розриву при видаленні єдиного ребра. Використання двозв'язних графів дуже важливо в області мереж (дивись потокова мережа), зважаючи на притаманну їм властивість резервування.
Визначення
Двозв'язний неорієнтований граф — це зв'язний граф, який не розпадається на частини при видаленні будь-якої вершини (і всіх інцидентних їй ребер).
Двозв'язний орієнтований граф — це такий граф, що для будь-яких двох вершин v і w є два орієнтованих шляхи з v в w, що не мають спільних вершин крім v і w.
| Число вершин | Число варіантів |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 3 |
| 5 | 10 |
| 6 | 56 |
| 7 | 468 |
| 8 | 7123 |
| 9 | 194066 |
| 10 | 9743542 |
| 11 | 900969091 |
| 12 | 153620333545 |
| 13 | 48432939150704 |
| 14 | 28361824488394169 |
| 15 | 30995890806033380784 |
| 16 | 63501635429109597504951 |
| 17 | 244852079292073376010411280 |
| 18 | 1783160594069429925952824734641 |
| 19 | 24603887051350945867492816663958981 |
Приклади
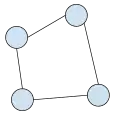Двозв'язний граф з 4-ма вершинами та 4-ма ребрами.
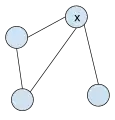Граф не є двозв'язним. Видалення вершини x розбиває граф.
Двозв'язний граф з 5-ма вершинами та 6-ма ребрами.
Граф не є двозв'язним. Видалення вершини x розбиває граф.
Посилання
- Eric W. Weisstein. "Biconnected Graph." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/BiconnectedGraph.html
- Paul E. Black, "biconnected graph", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 17 December 2004. http://www.nist.gov/dads/HTML/biconnectedGraph.html
Див. також
- Java-реалізація дерева двозв'язних компонент в jBPT бібліотеці (див. BCTree class).