Діаграма Пенроуза

Прямі лінії, що відповідають сталому часу та координаті є гіперболами, що виникають та збігаються в кутах діаграми. Ці точки являють собою "конформну безкінечність" для простору та часу.

Іноді ці діаграми називають ще діаграмами Пенроуза-Картера, на честь Бардона Картера та Роджера Пенроуза, що були першими, хто використовував ці даіграми у дослідженнях. Вони також називаються конформними діаграмами, або просто часопросторовими діаграмами.

Діаграма Пенроуза нескінченного всесвіту Мінковського, горизонтальна вісь u, виртикальна - v

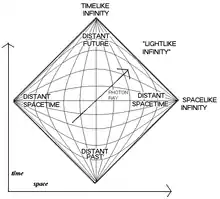
Дві лінії, накреслені під кутом 45°, повинні перетинатися на діаграмі, якщо відповідні два світлових промені перетинаються в справжньому часопросторі. Таким чином, діаграми Пенроуза використовують як лаконічну ілюстрацію для областей часопростору, придатних до спостереження. Діагональні гарничні лінії діаграми Пенроуза відповідають нескінченості або сингулярності, де мають закінчуватися світлові промені. Таким чином, ця техніка корисна при вивченні асимптотичних властивостей часопростору та сингулярностей. Нескінченно статичні координати простору Мінковського ${\displaystyle (x,t)}$ пов'язані з координатами Пенроуза ${\displaystyle (u,v)}$ наступним чином:

${\displaystyle \tan(u\pm v)=x\pm t}$

Кути "діаманту Пенроуза", що відповідають часо- та простороподібній конформним нескінченостям рівні ${\displaystyle \pi /2}$.

Діаграми Пенроуза часто використовуються для ілюстрації часопростору навколо чорних дір. Сингулярностям відповідає простороподібна границя, тоді як часоподібна границя відповідає звичайній просторово-часовій діаграмі. Це відповідає заміні часової та просторової координат на горизонт чорної діри (так як простір однонапрямлений всередині горизонту, а час однонапрямлений зовні горизонту). Сингулярність являє собою простороподібну границю і дає зрозуміти, що об'єкт, одного разу досягнувши горизонту, то він обов'язково потрапить в сингулярність, навіть якщо спробує від неї ухилитися.

Також Діаграми Пенроуза використовуються для ілюстрації часопростору навколо гіпотетичних червоточин, що пов'язують два окремі всесвіти, що є розширенням розв'язку Шварцшильда для чорних дір. Попередниками діаграм Пенроуза були діаграми Крускала-Секереша. Це також дало метод поділу горизонту подій на минуле та майбутнє та розщеплення сингулярності на минуле та майбутнє горизонтальними лініями (так як сингулярність "обрізає" всі шляхи до майбутнього, якщо вони потрапляють до чорної діри). Результатом є гіпотетичний об'єкт, що зветься сірою дірою, що, по суті, є білою дірою, що перетворюється на чорну діру після короткого відкриття червоточини, що з'єднує дві асимптотично пласкі часопросторові області, що звуться "всесвітами". Червоточина зачиняється (формуючи "майбутні" сингулярності) так швидко, що коридор між двома всесвітами вимагає надсвітлової швидкості, а тому є неможливим. Діаграми Пенроуза додали до діаграм Крускала-Секереша конформне стиснення областей плаского часо-простору далеко від діри.

Оскільки простороподібнй коридор статичної чорної діри подолати неможливо, діаграми Пенроуза для електрично заряджених чорних дір, що обертаються, дають "внутрішній горизонт подій" (що лежить в майбутньому) та вертикальні сингулярності, що відкривають так звані "часоподібні червоточини", дозволяючи прохід до майбутніх всесвітів. У випадку діри, що обертається, існує всесвіт з "від'ємною гравітацією", фіксований через сингулярність кільцевої форми (зображену, проте, лінією на діаграмі), яку можна подолати, якщо вхід до діри близький до осі обертання.

Виходячи з усього того, що стосується червоточин, деякі науковці стверджують, що:

1. Це не описує типову чорну діру, що утворюється внаслідок колапсу зорі.

2. Випромінювання при обертанні, синє зміщення світлових променів навколо чорної діри уможливлює проходження її наскрізь, а також робить можливим утворення нової сингулярності поза дірою.

• d'Inverno, Ray (1992). Introducing Einstein's Relativity. Oxford: Oxford University Press. ISBN 0-19-859686-3. See Chapter 17 (and various succeeding sections) for a very readable introduction to the concept of conformal infinity plus examples.
• Frauendiener, Jörg. Conformal Infinity. Living Reviews in Relativity. Архів оригіналу за лютий 23, 2004. Процитовано February 2, 2004.
• Carter, Brandon (1966). Complete Analytic Extension of the Symmetry Axis of Kerr's Solution of Einstein's Equations. Phys. Rev. 141 (4): 1242–1247. Bibcode:1966PhRv..141.1242C. doi:10.1103/PhysRev.141.1242. See also on-line version (requires a subscription to access)
• Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4. See Chapter 5 for a very clear discussion of Penrose diagrams (the term used by Hawking & Ellis) with many examples.
• Kaufmann, William J. III (1977). The Cosmic Frontiers of General Relativity. Little Brown & Co. ISBN 0-316-48341-9. Really breaks down the transition from simple Minkowski diagrams, to Kruskal-Szekeres diagrams to Penrose diagrams, and goes into much detail the facts and fiction concerning wormholes. Plenty of easy to understand illustrations. A less involved, but still very informative book is his William J. Kaufmann (1979). Black Holes and Warped Spacetime. W H Freeman & Co (Sd). ISBN 0-7167-1153-2.