Ефект Гуржи

Ефект Гуржи був теоретично передбачений [1] [2] Радієм Миколайовичем Гуржи в 1963 році. Він полягає в зменшенні електричного опору ${\displaystyle R}$ провідника кінцевих розмірів із підвищенням його температури ${\displaystyle T}$ (тобто ситуація ${\displaystyle dR/dT<0}$ для певного температурного інтервалу). Ефект Гуржи зазвичай розглядається як доказ гідродинамічного транспорту [3] [4] [5] [6] [7] [8] у провідних середовищах.

Ефект Гуржи
Названо на честь	Гуржи Радій Миколайович
Дата відкриття (винаходу)	1963
Формула	${\displaystyle R\propto l_{ee}(T)/d^{2}\propto T^{-5}d^{-2}}$

Показано різні режими транспорту зарядів. Блакитне коло – це електрон, що рухається в провіднику шириною d. Червоні зірки відповідають зіткненням із втратою повного імпульсу електрону..

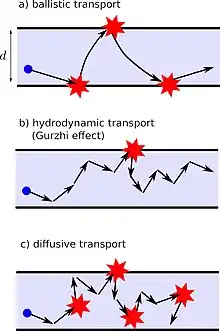
Механізм ефекту Гуржи наступний: Величина опору провідника обернена до ${\displaystyle l_{lost}=\min\{l_{boundary},l_{V}\}}$ — середня довжина вільного пробігу, що відповідає втраті імпульсу в системі електронів

$${\displaystyle R\propto {\frac {1}{l_{lost}}},}$$

де ${\displaystyle l_{boundary}}$ – середня відстань, яку проходить електрон між двома послідовним взаємодіями з границею, ${\displaystyle l_{V}}$ є середнім вільним пробігом, що відповідає іншим можливостям втрати імпульсу. Відбиття електронів від границі вважається дифузним.

При низьких температурах реалізується балістичний транспорт: ${\displaystyle l_{ee}\gg d}$, ${\displaystyle l_{lost}\approx l_{boundary}\approx d}$, де ${\displaystyle d}$ - ширина провідника, ${\displaystyle l_{ee}}$ є середнім вільним пробігом, що відповідає нормальним електрон-електронним зіткненням (тобто зіткненням без процесів перекиду імпульсу). При низьких температурах фонон, що випромінюється електроном, швидко взаємодіє з іншим електроном без втрати сумарного імпульсу електрон - фононної системи та ${\displaystyle l_{ee}\approx l_{ep}}$, де ${\displaystyle l_{ep}\propto T^{-5}}$ – середній вільний пробіг, що відповідає електрон - фононним зіткненням. Також ми припускаємо ${\displaystyle d\ll l_{V}}$ Таким чином, опір для найнижчих температур є постійною ${\displaystyle R\propto d^{-1}}$ (див. малюнок). Ефект Гуржи з'являється при підвищенні температури, коли довжина електрон-електронних зіткнень стає достатньо малою ${\displaystyle l_{ee}\ll d}$. У цьому режимі дифузійну довжину електронів між двома наслідками взаємодії з границею можна розглядати як вільний пробіг відносно втрат імпульсу. Користуючись відомими формулами броунівського руху, легко показати, що довжина траєкторії між двома зіткненнями з границею порядку ${\displaystyle l_{lost}\approx l_{boundary}\approx d^{2}/l_{ee}}$, а опір пропорційний ${\displaystyle R\propto l_{ee}(T)/d^{2}\propto T^{-5}d^{-2}}$. Таким чином, маємо від’ємну похідну ${\displaystyle dR/dT<0}$ . Тому ефект Гуржи можна спостерігати при ${\displaystyle l_{ee}\ll d\ll d^{2}/l_{ee}\ll l_{V}}$ .

Ефект Гуржи відповідає незвичайній ситуації, коли електричний опір залежить від частоти нормальних зіткнень. Як ми бачимо, цей ефект виникає через наявність границь зразка зі скінченним характерним розміром ${\displaystyle d}$ . Пізніше група Гуржи виявила особливу роль гідродинаміки електронів у спіновому транспорті. [9] [10] У такому випадку магнітна неоднорідність грає роль «межі» зі спін-дифузійною довжиною, [11] як характерного розміру замість ${\displaystyle d}$ , як раніше. Ця магнітна неоднорідність зупиняє електрони одного напрямку, і стає ефективним розсіювачем для електронів з протилежним спіном. У цьому випадку магнітоопір провідника залежить від частоти нормальних електрон-електронних зіткнень, а також від ефекту Гуржи.