Задача Кобона про трикутник
Задача Кобона про трикутник — невирішена задача з комбінаторної геометрії, яку сформулював Кодзабуро Фудзмура (Кобон), японський математик (1903—1983). Задача полягає у з'ясуванні, яке максимальне число трикутників, що не перекриваються, сторони якого належать конфігурації n прямих, можна утворити. Варіант задачі розглядається в проєктивній площині, а не в евклідовій площині, в цьому випадку вимагається, щоб трикутники не перетиналися іншими прямими.
Ідеальна конфігурація — це розташування прямих, які попарно перетинаються і кожен відрізок є стороною, а дві відповідні прямі є частиною щонайбільше двох пар трикутників, що мають спільну сторону.
Кобон знайшов найбільшу кількість трикутників , які не перекриваються та їх можна побудувати за допомогою ліній, тому трикутник Кобона визначається як один із трикутників, побудованих таким чином. Кілька перших — це 1, 2, 5, 7, 11, 15, 21, …
Аналітичний вираз для знаходження кількості трикутників вивів Сабуро Тамура.
Теорема Сабуро Тамура. забезпечує верхню межу максимальної кількості трикутників. Тому для 2,3, … перші кілька верхніх меж — це 2, 5, 8, 11, 16, 21, 26, 33, … .
Лема 1. Якщо (n mod 3) ∈ {0, 2}, то всі конфігурації, які відповідають верхній межі , є ідеальними конфігураціями. В цих випадках mod 3, а .
Лема 2. У ідеальній конфігурації усі екстремальні точки мають степінь 2.
Лема 3. Ідеальна конфігурація існує лише для непарних .
Г. Клемен та Дж. Бадер. знайшли більш чітку межу кількості трикутників Кобона:
Теорема Г. Клемена та Д. Бадера. Максимальна кількість трикутників Кобона для заданої кількості прямих в площині обмежені верхніми межами:
, де — індикатор функції. Тобто верхня межа за С.Тамури не можа бути досягнута для всіх з mod 6 mod 6.
Доведення. Відповідно до Леми 1 верхню межу можна досягти за допомогою конфігурацій, якщо mod 3 або mod 3. Але ці ідеальні конфігурації можливі тільки для непарного згідно Леми 3. Отже, для та не може досягати верхньої межі. Ці дві умови можна узагальнити як . Тоді:
А. Вайнберг знайшов конфігурацію для - 25 трикутників.
В 1967 р. конфігурацію з - 25 трикутників знайшов Б.Грюнбаум, а іншу конфігурацію - С.Хонма. Верхня межа означає, що максимум повинно бути 25 або 26 (невідомо, який). С.Хонма ілюстрував конфігурацію для - 32 трикутники, де 33 трикутники - це теоретично можливий максимум.
У 1996 році С.Грабарчуком і В.Кабановичем були знайдені два інші окремі рішення. У 1999 році В.Кабанович знайшов для , 38-трикутну конфігурацію (верхня межа дорівнює 40) і конфігурацію з 47 трикутників (яка відповідає верхній межі 47 трикутників).
Т.Судзукі знайшов конфігурацію для , яка є максимальною, оскільки вона задовольняє верхній межі .
Подальше дослідження виявило конфігурації для - 53 трикутників (верхня межа дорівнює 56), - 72 трикутники (74), а також - 85 трикутників - нове рішення, яке відповідає верхній межі.
Останній рядок таблиці показує нову прив'язку. Зірочка у рядку вказує оптимальні конфігурації на додаток до вже відомих оптимальних рішень (жирним шрифтом).
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| (n mod 6) | 3 | 4 | 5 | 0 | 1 | 2 | 3 | 4 | 5 | 0 | 1 | 2 | 3 | 4 | 5 | 0 | 1 | 2 |
| К(n) | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 25 | 32 | 38 | 47 | 53 | 65 | 72 | 85 | 93 | 104 | 115 |
| Верхня межа С.Тамури | 1 | 2 | 5 | 8 | 11 | 16 | 21 | 26 | 33 | 40 | 47 | 56 | 65 | 74 | 85 | 96 | 107 | 120 |
| Верхня межа Г.Клемена та Д.Бадера | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 26 | 33 | 39 | 47 | 55 | 65 | 74 | 85 | 95 | 107 | 119 |
Приклади
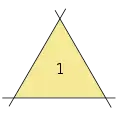 3 прямі дають один трикутник
3 прямі дають один трикутник 4 прямі
4 прямі 5 прямих
5 прямих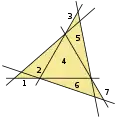 6 прямих
6 прямих 7 прямих
7 прямих
Література
- K. Fujimura, The Tokyo Puzzle Charles Scribner's Sons, New York, 1978.
- M. Gardner, Wheels, Life, and Other Mathematical Amusements. W. H. Freeman, New York, pp. 170—171 and 178, 1983. [4] E. Pegg, Math Games: Kobon Triangles
- Weisstein, Eric W. Трикутники Кобона(англ.) на сайті Wolfram MathWorld.
- https://sop.tik.ee.ethz.ch/publicationListFiles/cb2007a.pdf
- https://oeis.org/A006066