Задача про найкоротший шлях

В теорії графів, задача про найкоротший шлях полягає в знаходженні такого шляху між двома вершинами (або вузлами) графу, що сума ваг ребер з яких він складається мінімальна. Прикладом може бути знаходження найкоротшого шляху між двома пунктами на дорожній мапі; в цьому випадку, вершинами є пункти, а ребрами — відтинки дороги із вагами, рівними часу, необхідному для подолання цього відрізку.

(6, 4, 5, 1) і (6, 4, 3, 2, 1) є шляхами між вершинами 6 і 1

Найкоротший шлях (A, C, E, D, F) між вершинами A та F у зваженому орієнтованому графі

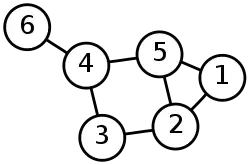
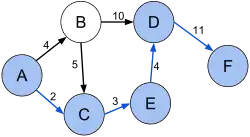
Формально, маємо зважений граф (це набір вершин V і ребер E з дійсно-значимою функцією ваги f : E → R), і заданим елементом v з V, знайти шлях P з v до v' з V такий, що

${\displaystyle \sum _{p\in P}f(p)}$

найменша серед усіх шляхів, що зв'язують v з v' .

Така задача іноді згадується як Задача про найкоротший шлях між парою вершин, щоб відрізнити від наступних узагальнень:

• Задача про найкоротші шляхи з одного входу, тут ми маємо знайти найкоротші шляхи між вхідною вершиною v та всіма іншими вершинами графу.
• Задача про найкоротші шляхи з одним виходом, тут ми маємо знайти найкоротші шляхи з усіх вершин графу до однієї вихідної v. Може бути зведена до задачі з одним входом шляхом зміни на зворотні ребер графу.
• Задача про найкоротші шляхи для всіх пар, тут ми маємо знайти найкоротші шляхи між кожною парою вершин v, v' в графі.

Ці узагальнення мають значно дієвіші алгоритми ніж спрощений підхід із запуском алгоритму пошуку найкоротшого шляху між всіма значимими парами вершин.