Квазі-Монте Карло методи
Квазі-Монте-Карло метод (з англ. Quasi-Monte Carlo Method) - метод чисельного інтегрування та вирішення деяких інших задач з використанням послідовностей з низьким рівнем невідповідності (так-звані квазі-випадкові послідовності або суб-випадкові послідовності). Це на противагу звичайному методу Монте-Карло, який заснований на послідовності псевдовипадкових чисел.
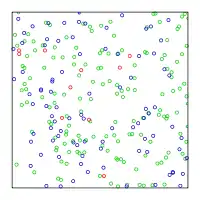

Методи Монте-Карло і квазі-Монте Карло викладені аналогічним чином. Проблема полягає в тому, щоб апроксимувати інтеграл від функції f як середнє значення функції, обчисленої в наборі точок х1, ..., хп:
Оскільки ми інтегруємо по х-вимірному одиничному кубі, кожен хi є вектором s елементів. Різниця між методами квазі-Монте-Карло і Монте-Карло - це спосіб вибору хi. Квазі-Монте-Карло використовує послідовності з низьким рівнем невідповідності, такі як послідовності Халтон, Соболеві послідовності, або послідовності Фора (з англ. Faure), в той час як метод Монте-Карло використовує псевдовипадкові послідовності. Перевага використання послідовностей з низьким рівнем невідповідності - швидкість збіжності. Метод квазі-Монте-Карло має оцінку збіжності О(1/n), тоді як у випадку методу Монте-Карло вона становить О(N-0.5).[1]
Метод квазі-Монте-Карло останнім часом став популярним в області математичних фінансів і фінансових обчислень. В цих областях багатовимірні числові інтеграли, де значення інтегралу повинне бути оцінене в межах порогового значення ε, трапляються часто. Методи Монте-Карло і квазі-Монте-Карло корисні в таких випадках.
Оцінка похибки апроксимації методу квазі-Монте Карло
Апроксимаційна похибка методу квазі-Монте-Карло обмежена значенням, пропорційним невідповідності комплекту х1, ..., хn. Зокрема, з нерівності Koksma-Hlawka маємо, що похибка
є обмеженою
- ,
де V(F) є варіацією Харді-Краузе для функції f (див. Morokoff і Кафлиш (1995) для детального визначення). Dn - це так звана головна розбіжність набору (х1,...,xn) і визначається як
- ,
де Q - прямокутна [0,1]s фігура зі сторонами, паралельними осям координат. Нерівність може бути використана, щоб показати, що похибка апроксимації методом квазі-Монте-Карло метод рівна , у той час як метод Монте-Карло має імовірнісну похибку . Хоча ми можемо тільки констатувати верхню межу похибки апроксимації, збіжність розрахунку методу квазі-Монте-Карло на практиці, як правило, набагато швидша за його теоретичну межу. Отже, в загальному випадку, точність методу квазі-Монте-Карло збільшується швидше, ніж збіжність методу Монте-Карло. Однак, ця перевага забезпечується тільки якщо N досить велике і якщо варіація скінченна.
Методи Монте-Карло та Квазі-Монте Карло для багатовимірних інтегрувань
Для одновимірного інтегрування, квадратурні методи, такі як методи трапецій, Сімпсона, або формула Ньютона–Котеса , відомі як ефективні, якщо функція є гладкою. Ці підходи можуть бути також використані для багатовимірної інтеграції, повторюючи одновимірні інтегрування за кількома вимірами. Однак кількість обчислень функції зростає експоненціально з числом вимірів s. Отже, щоб подолати це прокляття розмірності слід використовувати для багатовимірних інтегралів дещо інший метод. Стандартний метод Монте-Карло часто використовується, коли квадратурні методи складно або дорого реалізувати.[2] Методи Монте-Карло і квазі-Монте Карло точні і відносно швидкі, коли розмірність сягає 300 і вище.[3]
Мороков і Кафлиша вивчали продуктивність методів Монте-Карло і квазі-Монте Карло у інтегруванні. У статті, Халтон, Соболь, і Фор послідовності для квазі-Монте-Карло порівнюють із стандартним методом Монте-Карло з використанням псевдовипадкових послідовностей. Вони виявили, що метод з Халтон послідовністю найбільш ефективний для розмірностей до приблизно 6; метод з Соболевими послідовністями працює краще для більш високих розмірностей; і метод з Фор послідовностями, хоч і є гіршим за вказані дві інші послідновності, досі працює краще, ніж псевдовипадкові послідовності.
Однак, Мороков і Кафлиша навели приклади, де перевага методу квазі-Монте-Карло менша, ніж очікувалося теоретично. Ще, в прикладах вивчені Мороковим і Кафлишею, метод квазі-Монте-Карло не дає більш точний результат, ніж метод Монте-Карло з однаковою кількістю очок. Мороков і Кафлиша зауважили, що перевага методу квазі-Монте-Карло є значною, якщо під-інтегральний вираз є гладкою функцією, і кількість вимірів s інтегралу мала.
Недоліку методу квазі-Монте-Карло
Лем'є виділив недоліки методу квазі-Монте-Карло:[4]
- Для того щоб оцінка була меншою за , повинен бути достатньо малим і повинен бути великим (наприклад, ).
- Для багатьох функцій, що виникають на практиці, .
- Ми знаємо тільки верхню межу помилки (тобто ε ≤ V(f) DN), і важко обчислити і .
Для того, щоб подолати деякі з цих недоліків, ми можемо використати рандомізований метод квазі-Монте-Карло .
Рандомізування методу квазі-Монте Карло
Оскільки послідовності з низьким рівнем розбіжності не випадкові, а детерміновані, квазі-Монте-Карло метод може розглядатися як детермінований алгоритм або дерандомізований алгоритм. В даному випадку, у нас є тільки межа (наприклад, ε ≤ (Ф) ГН) похибки, і похибку важко оцінити. Для того, щоб уможливити аналіз та оцінку дисперсії, ми можемо рандомізувати метод (див. рандомізації для загального випадку). В результаті отримаємо рандомізований метод квазі-Монте-Карло, який також можна розглядати як зменшення варіації для стандартного методу Монте-Карло.[5] Серед декількох методів, найпростіша процедура перетворень - це через випадкові зміщення. Нехай {х1,...,хп} точка встановлена на послідовності з низькою розбіжністю. Оберемо випадковий s-вимірний вектор U і змішаємо його з {х1,...,хп}. Тобто, для кожного xJ, створюємо
і використовуємо послідовність замість . Якщо ми маємо R повторів за методом Монте-Карло, оберемо випадковий s-вимірний вектор U для кожної реплікації. Рандомізація дозволяє дати оцінку дисперсії, при цьому використовуючи квазі-випадкові послідовності. Порівняно з чисто методом квазі-Монте Карло, кількість зразків квазі-випадкової послідовності буде ділитись на R, рівноцінну за обчислювальних витрат, що зменшує теоретичну швидкість збіжності. У порівнянні зі стандартним методом Монте-Карло, дисперсії та обчислення швидкості є дещо кращі, ніж експериментальні результати у Туффина (2008) [6]
Див. також
Примітки
- Søren Asmussen and Peter W. Glynn, Stochastic Simulation: Algorithms and Analysis, Springer, 2007, 476 pages
- William J. Morokoff and Russel E. Caflisch, Quasi-Monte Carlo integration, J. Comput. Phys. 122 (1995), no. 2, 218--230. (At CiteSeer: )
- Rudolf Schürer, A comparison between (quasi-)Monte Carlo and cubature rule based methods for solving high-dimensional integration problems, Mathematics and Computers in Simulation, Volume 62, Issues 3–6, 3 March 2003, 509–517
- Christiane Lemieux, Monte Carlo and Quasi-Monte Carlo Sampling, Springer, 2009, ISBN 978-1441926760
- Moshe Dror, Pierre L’Ecuyer and Ferenc Szidarovszky, Modeling Uncertainty: An Examination of Stochastic Theory, Methods, and Applications, Springer 2002, pp. 419-474
- Bruno Tuffin, Randomization of Quasi-Monte Carlo Methods for Error Estimation: Survey and Normal Approximation, Monte Carlo Methods and Applications mcma.
- R. E. Caflisch, Monte Carlo and quasi-Monte Carlo methods, Acta Numerica vol. 7, Cambridge University Press, 1998, pp. 1–49.
- Josef Dick and Friedrich Pillichshammer, Digital Nets and Sequences. Discrepancy Theory and Quasi-Monte Carlo Integration, Cambridge University Press, Cambridge, 2010, ISBN 978-0-521-19159-3
- Michael Drmota and Robert F. Tichy, Sequences, discrepancies and applications, Lecture Notes in Math., 1651, Springer, Berlin, 1997, ISBN 3-540-62606-9
- William J. Morokoff and Russel E. Caflisch, Quasi-random sequences and their discrepancies, SIAM J. Sci. Comput. 15 (1994), no. 6, 1251–1279 (At CiteSeer:)
- Harald Niederreiter. Random Number Generation and Quasi-Monte Carlo Methods. Society for Industrial and Applied Mathematics, 1992. ISBN 0-89871-295-5
- Harald G. Niederreiter, Quasi-Monte Carlo methods and pseudo-random numbers, Bull. Amer. Math. Soc. 84 (1978), no. 6, 957–1041
- Oto Strauch and Štefan Porubský, Distribution of Sequences: A Sampler, Peter Lang Publishing House, Frankfurt am Main 2005, ISBN 3-631-54013-2
Зовнішні посилання
- The MCQMC Wiki page contains a lot of free online material on Monte Carlo and quasi-Monte Carlo methods
- A very intuitive and comprehensive introduction to Quasi-Monte Carlo methods
Статтю перекладено за ініціативи студентів факультету прикладної математики та інформатики ЛНУ ім. Франка http://www.lnu.edu.ua
Коментарі
Лінки не містять посилання на інші статті, допущено орфографічні помилки.