Ковзна симетрія
Ковзна симетрія — ізометрія Евклідової площини: комбінація відбиття відносно прямої і перенесення на вектор паралельний до . Зміна порядку операцій дає той самий результат. Іноді, ми можемо вважати відбиття окремим випадком ковзної симетрії з нульвим вектором паралельного перенесення.
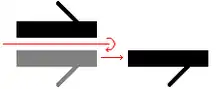
Приклад ковзної симетрії

Завдяки тому, що відбитки стоп мають симетрію ковзного відбиття, застосування операції ковзного відбиття відобразить кожен лівий відбиток в правий відбиток і навпаки, що приведе до конфігурації невідрізненної від початкової.
Ковзну симетрію можна представити у вигляді 3 осевих симетрій.[1]
Примітки
- Martin, George E. (1982). Transformation Geometry: An Introduction to Symmetry. Undergraduate Texts in Mathematics. Springer. с. 64. ISBN 9780387906362..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.