Кут падіння (оптика)
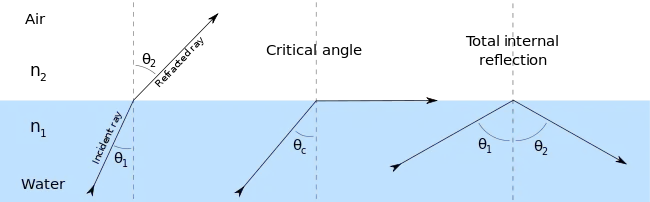
В геометричній оптиці кут падіння — це кут між променем, що падає на поверхню, і прямою, перпендикулярною до поверхні в точці падіння, що називається нормаллю. Промінь може утворюватися будь-якою хвилею: оптичною, акустичною, мікрохвильовою, рентгенівською тощо. На малюнку нижче лінія, що зображає промінь, утіорює кут θ з нормаллю (пунктирна лінія). Кут падіння, за якого світло починає повністю відбиватися, називається критичним кутом. Кут відбиття і кут заломлення — інші кути, пов'язані з променями.
Визначення кута відбиття відносно плоскої поверхні є тривіальним, але обчислення для майже будь-якої іншої поверхні значно складніше. Точне розв'язання для сфери (який має важливе застосування в астрономії та комп'ютерній графіці) був відкритою проблемою, поки результат не був отриманий математиками Алленом Р Міллером та Емануелем Вегом 1991 року.[1]
Кут ковзання
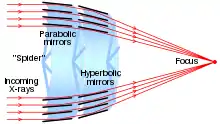
Маючи справу з пучком, який майже паралельний поверхні, іноді корисніше посилатися на кут між променем і поверхнею, а не на кут між променем і нормаллю, тобто на кут величиною 90° мінус кут падіння. Цей невеликий кут називають кутом ковзання (англ. glancing angle або grazing angle). Падіння під кутом ковзання називається «ковзним падінням». Кут ковзання — це кут, утворений падаючим променем або відбитим променем і площиною (поверхнею).
Ковзна дифракція застосовується в рентгенівській спектроскопії та атомній оптиці, де значне відбиття може бути досягнуте лише за малих значень кута ковзання. Дзеркала Френеля призначені для відбивання атомів, що надходять під малим кутом ковзання. Цей кут зазвичай вимірюється в мілірадіанах. В оптиці застосовується також дзеркало Ллойда .
Див. також
Примітки
- Allen R Miller and Emanuel Vegh (1993). Exact Result for the Grazing Angle of Specular Reflection from a Sphere. SIAM Review 35: 472–480. doi:10.1137/1035091.
Посилання
- Weisstein, Eric W. Angle of incidence(англ.) на сайті Wolfram MathWorld.
- geometry: rebound on the strip billiards Flash animation