Марковське покриття

У машинному навчанні ма́рковське покриття́ (англ. Markov blanket) вузла ${\displaystyle A}$ баєсової мережі — це множина вузлів ${\displaystyle \partial A}$, складена з батьківських вузлів ${\displaystyle A}$, його дочірніх вузлів, та інших батьківських вузлів його дочірніх вузлів. У марковському випадковому полі марковське покриття вузла — це множина його сусідніх вузлів. Марковське покриття може також позначатися через ${\displaystyle MB(A)}$.

У баєсовій мережі марковське покриття вузла A включає його батьків, дітей, та інших батьків усіх його дітей.

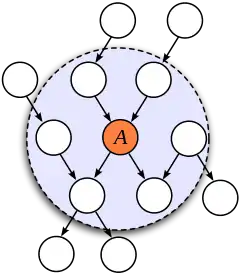
Будь-яка множина вузлів мережі є умовно незалежною від ${\displaystyle A}$, будучи обумовленою множиною ${\displaystyle \partial A}$, тобто, будучи обумовленою марковським покриттям вузла ${\displaystyle A}$. Ймовірність володіє марковською властивістю; формально, для різних вузлів ${\displaystyle A}$ та ${\displaystyle B}$

${\displaystyle \Pr(A\mid \partial A,B)=\Pr(A\mid \partial A).\!}$

Марковське покриття вузла містить всі змінні, які екранують цей вузол від решти мережі. Це означає, що марковське покриття вузла є єдиним знанням, потрібним для передбачування його поведінки. Цей термін було запроваджено Перлом 1988 року.[1]

У баєсовій мережі значення батьків та дітей вузла, очевидно, дають інформацію про цей вузол; проте батьків його дітей також має бути включено, оскільки вони можуть застосовуватися для пояснення даного вузла. У марковському випадковому полі марковське покриття вузла є просто його сусідніми вузлами.