Вершина (теорія графів)

Вершиною в теорії графів називається базовий елемент, який використовується при побудові графу: неорієнтований граф складається з множини вершин і множини ребер (невпорядкованих пар вершин), в той час як орієнтований граф складається з множин вершин і множин дуг (впорядкованих пар вершин). На малюнках, що представляють граф, вершина зазвичай представляється кружком з міткою, а ребро представляється лінією (дугою-стрілкою), що з'єднує вершини.

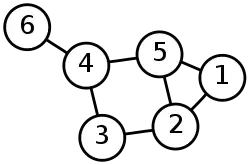
Граф з 6 вершинами і 7 ребрами, в якому вершина з номером 6 у лівому верхньому куті — лист, або висяча вершина

З точки зору теорії графів, вершини розглядаються як позбавлені характерних рис неподільні об'єкти, хоча вони можуть представляти деякі структури, залежні від проблеми, з якої пов'язаний граф. Наприклад, семантична мережа — це граф, в якому вершини представляють поняття класу об'єктів.

Дві вершини, що утворюють ребро називаються кінцевими вершинами ребра, і кажуть, що ребро інцидентне цим вершинам. Кажуть, що вершина w суміжна іншій вершині v, якщо існує граф, що містить ребро (v, w). Околом вершини v називається породжений підграф, утворений усіма вершинами, суміжними v.

Типи вершин

Степенем вершини графу називається число ребер, інцидентних їй. Вершина називається ізольованою, якщо її ступінь дорівнює нулю. Тобто, це вершина, яка не є кінцевою ні для якого ребра. Вершина називається листом (або висячою), якщо вершина має степінь одиниця. В орієнтованому графі розрізняють напівстепені виходу (число вихідних дуг) і напівстепені заходу (число вхідних ребер). Джерелом називається вершина з нульовим напівстепенем заходу, а вершина з нульовим степенем виходу називається стоком. Вершина називається симпліціальною, якщо всі сусідні їй вершини утворюють кліку: кожні два сусіди з'єднані. Універсальна вершина з'єднана з будь-якою вершиною графу.

Розділяючою вершиною або шарніром називається вершина, видалення якої приводить до збільшення кількості компонент зв'язності графу. Вершинним сепаратором називається набір вершин, видалення яких призводить до збільшення компонент зв'язності графу. k-вершинно-зв'язний граф — це граф, в якому видалення менш ніж k вершин завжди залишає граф зв'язним. незалежною множиною називається множина вершин, ніякі дві з яких не є суміжними, а вершинним покриттям називається множина вершин, яка включає хоча б одну кінцеву вершину будь-якого ребра графу. Векторним простором вершин графу називається векторний простір, що має як базис вектори, що відповідають вершинам графу (над полем чисел {0, 1}).[1][2]

Граф називається вершинно-транзитивним, якщо він має симетрії, які переводять будь-яку вершину в будь-яку іншу вершину. У контексті перерахування графу та ізоморфізму графів важливо розрізняти помічені вершини і непомічені вершини. Помічена вершина — це пов'язана з вершиною додаткова інформація, яка дозволяє відрізнити її від інших помічених вершин. Два графу можна вважати ізоморфними тільки тоді, коли ізоморфізм переводить вершини в вершини, що мають однакові мітки. Непомічені вершини можуть при цьому переводитися в інші вершини, ґрунтуючись тільки на суміжності і не використовуючи додаткову інформацію.

Вершини графу аналогічні вершинам багатогранника, але це не те ж саме — кістяк багатогранника утворює граф, вершини якого є вершинами багатогранника, але вершини багатогранника мають додаткову структуру (геометричне місце розташування), яка ігнорується в теорії графів. Вершина фігури багатогранника аналогічна околу вершини графу.

Див. також

Примітки
  1. М. Свами, К. Туласимаран. Графы, сети и алгоритмы. — Москва : Мир, 1984. — С. 62-76. глава 4
  2. Рейнгард Дистель. Теория графов. — Новосибирск : Издательство Института Математики, 2002. — С. 35.

Посилання
  • Gallo, Giorgio; Pallotino, Stefano (1988). Shortest path algorithms. Annals of Operations Research 13 (1): 1–79. doi:10.1007/BF02288320.
  • К. Берж. Теория графов и её применение. — Москва, 1962.
  • Chartrand, Gary (1985). Introductory graph theory. New York: Dover. ISBN 0-486-24775-9.
  • Biggs, Norman; Lloyd, E. H.; Wilson, Robin J. (1986). Graph theory, 1736-1936. Oxford [Oxfordshire]: Clarendon Press. ISBN 0-19-853916-9.
  • Harary, Frank (1969). Graph theory. Reading, Mass.: Addison-Wesley Publishing. ISBN 0-201-41033-8.
  • Harary, Frank; Palmer, Edgar M. (1973). Graphical enumeration. New York, Academic Press. ISBN 0-12-324245-2.
  • Weisstein, Eric W. Graph Vertex(англ.) на сайті Wolfram MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.