Модель Рауза

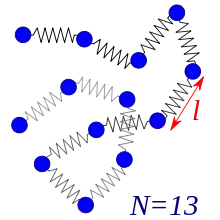
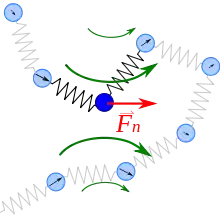
Полімер моделюється намистинками, кожна з яких з'єднана з сусідніми пружинками з жорсткістю k. Вважається, що намистинки рухаються у в'язкому середвищі — крім пружні сили на них діють сили тертя, ефект яких домінує над коливаннями намистинок, а також випадкова сила, як у рівнянні Ланжевена. Рівняння руху для n-тої намистинки записується:

${\displaystyle {\frac {\mathrm {d} {\vec {R}}_{n}}{\mathrm {d} t}}={\frac {k}{\zeta }}\cdot \left({\vec {R}}_{n-1}-{\vec {R}}_{n}+{\vec {R}}_{n+1}-{\vec {R}}_{n}\right)+{\vec {f}}_{n}(t).}$

Тут ${\displaystyle {\vec {R}}_{n}}$ — радіус-вектор n-тої намистинки, ${\displaystyle \zeta }$ — коефіцієнт тертя, ${\displaystyle {\vec {f}}_{n}(t)}$ — випадкова сила.

Розрахований за моделлю коефіцієнт дифузії обернено пропорційний числу намистинок у полімерному ланцюжку, тобто молекулярній масі полімеру:

${\displaystyle D_{G}={\frac {k_{B}T}{N\zeta }},}$

де ${\displaystyle k_{B}}$ — стала Больцмана, а ${\displaystyle T}$ — абсолютна температура.

Час обертової релаксації задається формулою:

${\displaystyle \tau _{R}={\frac {\zeta N^{2}l^{2}}{3\pi ^{2}k_{B}T}},}$

де ${\displaystyle l}$ — середня відстань між намистинками, ${\displaystyle Nl}$ — довжина розгорнутого в лінію полімерного ланцюжка.

Середньоквадратине зміщення за час ${\displaystyle \tau }$:

${\displaystyle \left\langle {\vec {R}}_{n}^{2}(\tau )\right\rangle =\left\langle \left({\vec {R}}_{n}(t+\tau )-{\vec {R}}_{n}(t)\right)^{2}\right\rangle \approx {\frac {2Nl^{2}}{\pi ^{3/2}}}{\sqrt {\frac {\tau }{\tau _{R}}}}.}$

Ілюстрація гідростатичної взаємодії.

У 1956 році Бруно Зімм удосконалив модель Рауза, врахувавши гідростатичні сили, що діють на полімер з боку розчинника[2]. В цій моделі коефіцієнт дифузії обернено пропорційний ${\displaystyle N^{\nu }}$, де ${\displaystyle \nu }$ — показник Флорі, який у конретному випадку дорівнює 1/2.

У моделі Зімма рівняння руху має вигляд:

${\displaystyle {\frac {\mathrm {d} {\vec {R}}_{n}}{\mathrm {d} t}}=k\cdot \sum \limits _{m}\mathrm {H} _{nm}\left({\vec {R}}_{n-1}-{\vec {R}}_{n}+{\vec {R}}_{n+1}-{\vec {R}}_{n}\right)+{\vec {f}}_{n}(t).}$

Тут замість єдиного коефіцієнта тертя вводиться матриця взаємодії ${\displaystyle \mathrm {H} _{nm}}$.

Це змінює коефіцієт дифузії до

${\displaystyle D_{G}={\frac {8k_{B}T}{3{\sqrt {6\pi ^{3}}}\eta _{s}{\sqrt {N}}\cdot l}}.}$

де η_s — в'язкість.

Час обертової релаксації стає:

${\displaystyle \tau _{R}={\frac {\eta _{S}({\sqrt {N}}l)^{3}}{{\sqrt {3\pi }}k_{B}T}},}$

а середньоквадратичне зміщення;

${\displaystyle \left\langle {\vec {R}}_{n}^{2}(\tau )\right\rangle ={\frac {2\Gamma (1/3)Nl^{2}}{\pi ^{2}}}\left({\frac {\tau }{\tau _{R}}}\right)^{2/3}.}$