Закон Гука
Закон Гука встановлює лінійну залежність між деформаціями та механічними напруженнями. Назву отримав на честь відкривача, англійського фізика XVII століття Роберта Гука. Закон Гука справедливий для малих пружних деформацій.
Математичний опис
Прості деформації
У своїй найпростішій формі закон Гука записується для визначення деформації довгого тонкого стрижня або пружини.
Розтяг/стиск
Для розтягу/стискання закон записується як:
- ,
де F — сила, k — коефіцієнт жорсткості, — видовження. Знак мінус показує, що сила напрямлена у протилежний бік до деформації. У цій формулі коефіцієнт жорсткості — це властивість стрижня, а не матеріалу, з якого він виготовлений. Він залежить від матеріалу, але також залежить від довжини стрижня, площі його перерізу, і, якщо мова йде про пружину, від її форми (діаметру і відстані між витками).
Коефіцієнт жорсткості стрижня довжиною і площею перерізу пов'язаний з модулем Юнга як[1]:
Варто зазначити, що межі застосування закону Гука для розтягу і стиску можуть сильно відрізнятися: такі матеріали як дерево витримують значно більші напруження при розтягу, ніж при стиску, у той час як метали або цемент — навпаки[2].
Зсув
Закон Гука для зсуву:
- ,
де N — модуль зсуву, — кут зсуву, а — площа поперечного перерізу (перпендикулярного напрямку зсуву)[3].
Інший варіант запису цієї формули[3]:
- ,
де — дотична напруга
Кручення
Для кручення, що є особливим видом зсуву, закон Гука записується як[3]:
- ,
де — момент сили, — модуль кручення а — кут кручення.
Модуль кручення у випадку кручення циліндра радіусом і висотою , пов'язаний з модулем зсуву як[3]:
Згин
Для згину можна сформулювати наступний аналог закону Гука[4]:
- ,
де — кривина нейтральної осі стрижня, а — момент інерції стрижня відносно цієї осі.
Потенціальна енергія деформованого тіла
Можна визначити потенціальну енергію стиснутої або розтягнутої пружини, що підкоряється закону Гука, інтегруючи рівняння x. Вона буде дорівнювати:
Аналогічний вигляд мають формули для потенціальної енергії і для інших типів деформації.
Складні напружені стани
Будь-яку деформацію можна розкласти як комбінацію деформацій розтягу-стиску і зсуву, тому закон Гука для тривимірного (складного) напруженого стану у випадку ізотропного матеріалу може бути записаний у вигляді системи рівнянь, що містить три рівняння для деформацій розтягу-стиску:
де ε — Відносне видовження вздовж осі, — коефіцієнт Пуассона, σ — напруження розтягу-стиску, E — модуль Юнга.
І три рівняння для деформацій зсуву:
де γ — кут зсуву в точці, τ — напруження зсуву в точці, G — модуль зсуву.
У більш компактній формі закон можна сформулювати так: компоненти тензора деформації в даній точці тіла знаходяться в лінійній залежності від компонентів тензора напруження тієї ж точки.
- ,
де — тензор механічних напружень, — тензор деформації, а — тензор четвертого рангу, який називається тензором модулів пружності і є характеристикою речовини.
Формулювання через напруження
Механічним напруженням називають міру внутрішніх сил, що виникають у твердому тілі при його деформації. Чисельно напруження дорівнює відношенню сили, що діє на невелику ділянку всередині тіла, до площі цієї ділянки(таким чином, одиницею вимірювання напруження є паскаль). Напруження має деяке значення у кожній точці всередині тіла, і деякою мірою є подібним до тиску у газах чи рідинах, але, на відміну від тиску, є векторною величиною. У тих межах, де закон Гука виконується, напруження прямо пропорційне відносному видовженню. Коефіцієнт пропорційності між цими величинами не залежить від форми або розмірів об'єкту, а лише від матеріалу, з якого він зроблений. Цей коефіцієнт називається модулем Юнга[5].
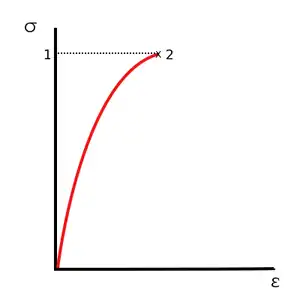
Межі застосування закону
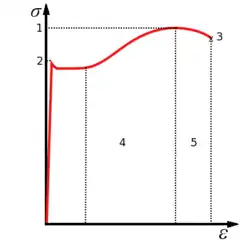
Важливим загальним обмеженням закону Гука є те, що він діє лише у частині діапазону можливих деформацій. Максимальне напруження, при якому він виконується називається границею пропорційності. Варто зазначити, що границя пропорційності нижча від границі пружності, хоча зазвичай ці точки близькі — тобто, існує такий діапазон деформації, при якому зберігається еластичність (тобто, при зніманні напруги тіло повертається до свого початкового стану), але при цьому рівняння зв'язку між видовженням і напруженням стає нелінійним[6]. Також, треба пам'ятати, що закон Гука порушується не різко, натомість відхилення від нього поступово наростають — таким чином, межа пропорційності може змінюватися в залежності від необхідної точності.

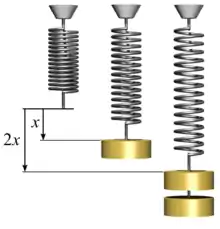
Також, конкретні пружини можуть мати особливості конструкції, через які їх реакція на деформацію не підкоряється закону Гука. Основні типи негуківських пружин[7]:
- Пружини зі змінним радіусом — конічні або біконусні (типу пісочного годинника або сочевиці). Напруження в такій пружині зростає швидше ніж розтяг. Хоча у ній також можна виділити невеликий діапазон пропорційного зростання, нелінійність починається при напруженнях у кілька разів нижчих за границі еластичності[8].
- Пружини зі змінним кроком — найчастіше така пружина складається з двох або більше частин, кожна з яких має різну відстань між витками. У такому випадку діаграма залежності напруження від розтягу також складається з кількох лінійних ділянок, кожна з яких має свій кут нахилу. Ділянки впорядковані так, що коефіцієнт жорсткості є більшим для більших деформацій. Те ж стосується і випадку, якщо дві неоднакові пружини поєднані послідовно[7].
- Переднапружені (попередньо напружені) пружини. Такі пружини є напруженими навіть якщо ніякі зовнішні сили на них не діють. Завдяки цьому графік залежності напруження від розтягу починається не з нуля, а з деякої величини, що визначається попереднім напруженням[7]. Підтипом таких пружин є пружини постійної сили, попередньо напружені пружини кручення з низьким коефіцієнтом жорсткості, сила пружності яких порівняно слабко змінюється у робочому діапазоні[9].
Закон Гука ніяк не враховує час, протягом якого була прикладена сила. Тобто, у ідеальному гуківському матеріалі, при постійній прикладеній силі деформація буде завжди лишатися однаковою. В реальності, при постійному напруженні матеріал з часом зазнає невеликих додаткових деформацій. Це явище називається повзучістю. Різні матеріали по різному піддаються таким деформаціям. Метали є не дуже повзучими, а такі матеріали як дерево, бетон, тканини, канати — помітно деформуються з часом. При підвищенні температури і напружень повзучість проявляється і для металів. Для кожного матеріалу існує деяке критичне напруження, при перевищенні якого повзучі деформації з часом ростуть необмежено аж до руйнування[10].
Для деяких м'яких матеріалів біологічного походження, закон Гука не виконується. Напруження у них може практично не змінюватися при деформації, аж до значних видовжень у 50%. У багатьох біологічних тканинах, таких як судини, після досягнення деякого критичного рівня деформації, напруження починає стрімко зростати, що не дозволяє їм змінювати розміри занадто сильно. А у рідких тканин, таких як слина, такої зміни не відбувається, і напруження залишається сталим[11].
Природа закону Гука
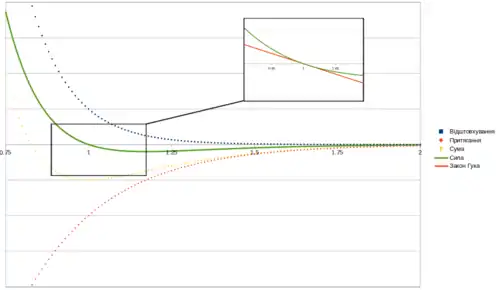
У твердому тілі існують міжатомні сили двох типів: притягування і відштовхування. Енергія взаємодії у обох випадках швидко зростає, якщо атоми знаходяться дуже близько, і до нуля, якщо вони віддаляються. Проте сили відштовхування спадають швидше, ніж сили притягання. Наприклад, у поширеному простому потенціалі міжатомної взаємодії, потенціалі Морзе, сили притягання і відштовхування спадають експоненціально зі збільшенням відстані, проте експонента для сил відштовхування спадає вдвічі швидше. Це призводить до того, що існує відстань, на якій сума потенціалів притягання і відштовхування набуває мінімального значення, і за відсутності сторонніх сил атоми розміщуються саме на цій відстані один від одного. При розтягуванні тіла, відстань між його атомами збільшується, атоми виходять з положення рівноваги, і їх потенціальна енергія збільшується. Відповідно, між атомами виникає сила, що дорівнює
Закон, що описує цю силу є складним, проте, як можна бачити на діаграмі, якщо відносне видовження не перевищує кількох відсотків, графік цієї сили є лінійним. Саме у цій області і застосовується закон Гука[12].
Наведена вище схема працює у більшості пружних твердих тіл — форма потенціалу взаємодії є подібною для всіх, хоча межі застосування закону Гука і модулі еластичності сильно залежать від конкретного вигляду функції потенціалу. Проте, для еластомерів, таких як гуми, природа еластичності є іншою, ентропійною. Завдяки ентропійним силам вони мають надзвичайно низьку жорсткість і можуть розтягуватися на сотні відсотків без руйнування. При розтягуванні еластомера, робота витрачається на збільшення члену у формулі вільної енергії, а не на збільшення відстані між атомами[12].
Використання
Невдовзі після відкриття закону Гука він знайшов використання у балансових механізмах годинників, що дозволило зробити їх більш точними і транспортабельними. Також, зв'язок розтягу пружини і сили використовується у багатьох вимірювальних приладах, таких як динамометри і манометри. Також, це рівняння використовується у багатьох галузях механіки, для розрахунку зміни розмірів твердих тіл під навантаженням, наприклад для сейсмостійкого будівництва або ж для врахування акустичних ефектів[13].
Історія
У 1658 році Роберт Гук почав працювати над проблемою збільшення точності годинників за допомогою спіральних пружин[14]. У 1660 році він сформулював закон, що пов'язував видовження тіла і силу пружності[15]. У 1676 році він опублікував його у вигляді анаграми, «ceiiinosssttuu», а у 1678 розкрив її рішення — фразу латиною «ut tensio sic vis», що можна перекласти як «сила така, як і видовження». Тоді ж він опублікував «Лекцію про пружини», де в деталях пояснював цей закон[16]. Цікаво, що у своїх лекціях Гук не зосереджувався лише на пружності твердих тіл, але формулював закони і для пружності рідких тіл і газів.
Результати роботи Гука з годинниками викликали несподівану суперечку. Ймовірно, він винайшов спіраль балансу ще у 1670 році, на 5 років раніше за Християна Гюйгенса, проте протоколи засідань Королівського товариства, де він розповів про свій винахід, за кілька років до і після 1670-го були втрачені, тому підтвердити цей факт не вдалося. У 20 столітті відповідні документи були знайдені у архіві самого Гука — ймовірно, він вилучив їх невдовзі після виступу, оскільки параноїдально боявся, що його відкриття будуть вкрадені[17].
У формулюванні самого Гука, закон мав не дуже велику користь, оскільки коефіцієнт жорсткості визначався для конкретного об'єкту, і не міг бути вирахуваним. Лише у 1822 році Огюстен-Луї Коші ввів поняття механічного напруження, що дало загальний підхід до задач обрахування пружних властивостей об'єктів (до того протягом 150 років ця задача була хоча б частково вирішена лише для кількох окремих випадків). Також у 20-х роках завдяки роботам Томаса Юнга і Клода-Луї Нав'є було введене сучасне поняття модуля пружності(модуля Юнга)[5].
Див. також
Примітки
- ЗАКОН ГУКА
- Гордон, 1980, Розділ 12.
- Визначення модуля зсуву із кручення
- РОЗРАХУНКИ НА МІЦНІСТЬ І ЖОРСТКІСТЬ СТЕРЖНІВ ПРИ ПЛОСКОМУ ЗГИНІ
- Гордон, 1980, Розділ 2.
- Elastic limit(англ.)
- It's Spring Time Part 3: Load-Deflection Relationships(англ.)
- Ends Effect on Conical Spring Behavior(англ.)
- Constant Force Springs(англ.)
- Гордон, 1980, Розділ 6.
- Гордон, 1980, Розділ 7.
- Young's modulus, Hooke's law and material properties (англ.)
- What is Hooke's Law?(англ.)
- Robert Hooke, Hooke's Law & the Watch Spring(англ.)
- Hooke's law(англ.)
- Elasticity Relations(англ.)
- Settling the 300-Year Old Dispute — Who Invented the Balance Spring? (англ.)
Література
- Гука закон // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 74. — ISBN 978-966-7407-83-4.
- Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993 .- 655 с. ISBN 5-11-004083-5
- Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб'юк В. І. — К., 2009. — 380 с.
- Мильніков О. В. Опір матеріалів. Конспект лекцій / Олександр Володимирович Мильніков. − Тернопіль: Видавництво ТНТУ, 2010. − 257 с.
Д. Гордон. Конструкции, или почему не ломаются вещи. — Суми : «МИР», 1980. — 390 с.