Монотонний многокутник

У геометрії, многокутник P на площині називають монотонним щодо прямої L, якщо кожна лінія ортогональна до L перетинала P щонайбільше двічі.[1]

Зелене позначає один перетин, синє позначає два перетини і червоне позначає три або більше. Два горішні многокутники монотонні щодо L, тоді як інші — ні.

Подібно, ламану C звуть монотонною щодо прямої L, якщо кожна лінія ортогональна з L перетинає C щонайбільше раз.

Для багатьох практичних цілей це визначення можна розширити, щоб дозволити випадки коли деякі ребра P ортогональні з L, і простий многокутник можна назвати монотонним якщо відрізок прямої, що поєднує дві точки в P і є ортогональним з L повністю належить P.

Властивості

Якщо припустити, що L збігається з віссю x. Тоді найлівіша і найправіша вершини монотонного многокутника розбивають його границю на дві монотонні ламані, такі що коли вершини будь-якої ламаної перебирати в їхньому природному порядку, то їхні x-координати монотонно зростають або спадають. Насправді, цю властивість можна взяти за визначення монотонного многокутника і вона дає йому свої ім'я.

Опуклий многокутник є монотонним щодо будь-якої прямої і многокутник монотонний щодо будь-якої прямої є опуклим.

Відомий алгоритм лінійного часу, що видає всі напрямки у яких певний простий многокутник є монотонним.[2] Його узагальнили так, щоб він повідомляв усі способи розкладення простого многокутника на дві монотонні ламані (можливо монотонні в різних напрямках.)[3]

Запити на належність точки многокутнику у випадку монотонного многокутника можна обробити за логарифмічний час після передобробітку лінійного часу (щоб знайти найлівішу і найправішу вершини).[1]

Монотонний полігон можна легко тріангулювати за лінійний час за допомогою алгоритму А. Фурньє і Д. Я. Монтуно,[4] або алгоритмом Годфріда Туссена.[5]

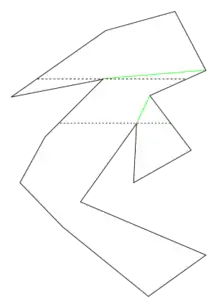
Розбиття многокутника на монотонні частини

Простий полігон можна легко розбити на монотонні полігони за час O(n log n). Однак, оскільки трикутник це монотонний многокутник, то тріангуляція многокутника розбиває многокутник на монотонні многокутники, і, у випадку простого многокутника, її можна зробити за час O(n).

Примітки
  1. Препарата, Франко; Шеймос, Майкл (1985). Computational Geometry – An Introduction. Springer-Verlag. ISBN 0-387-96131-3. 1ша редакція: ISBN 0-387-96131-3; 2ге видання, виправлене і довнене.
  2. Препарата, Франко; Суповіт, Кеннет (1981). Testing a simple polygon for monotonicity. Information Processing Letters 12 (4): 161–164. doi:10.1016/0020-0190(81)90091-0..
  3. Раппапорт, Девід; Розенблум, Арнольд (1994). Moldable and castable polygons. Computational Geometry 4 (4): 219–233. doi:10.1016/0925-7721(94)90020-5..
  4. Fournier, A.; Montuno, D. Y. (1984). Triangulating simple polygons and equivalent problems. ACM Transactions on Graphics 3 (2): 153–174. ISSN 0730-0301. doi:10.1145/357337.357341.
  5. Toussaint, Godfried T. (1984), "A new linear algorithm for triangulating monotone polygons," Pattern Recognition Letters, 2 (March):155–158.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.