Належність точки многокутнику

Стандартний метод визначення належності точки простому многокутнику полягає в наступному. Випускається промінь з цієї точки в довільному напрямку (при реалізації алгоритму зручно вибрати позитивний напрямок горизонтальної осі ${\displaystyle Ox}$), і рахується скільки разів промінь перетинає ребра многокутника. Для цього достатньо пройтися в циклі по ребрах многокутника і визначити, чи перетинає промінь кожне ребро. Якщо кількість перетинів непарна, то оголошується, що точка лежить всередині многокутника, якщо парна — то зовні. Метод засновано на тому простому спостереженні, що при русі по променю з кожним перетином кордону точка поперемінно виявляється то всередині, то зовні многокутника.

В алгоритмі виникає ускладнення в виродженому випадку, коли промінь перетинає вершину многокутника. Один зі способів його подолання полягає в тому, щоб вважати, що такі вершини многокутника лежать на нескінченно малу відстань вище (або нижче) променя, тоді будуть відсутні перетини в вершині. Таким чином, перетин променя з ребром зараховується, якщо кінці ребра лежать по різні боки від променя.

Алгоритм працює за час ${\displaystyle O(N)}$ для ${\displaystyle N}$-кутника.

Належність точки опуклому або зірчастому ${\displaystyle N}$-кутнику може бути визначена за допомогою двійкового пошуку за час ${\displaystyle O(\log N)}$, при витраті ${\displaystyle O(N)}$ пам'яті та ${\displaystyle O(N)}$ часу на попередню обробку.

Внутрішні точки мають різні індекси

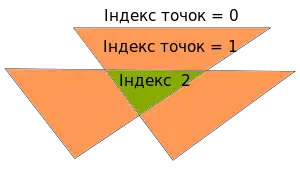
Цей метод базується на понятті індексу контуру відносно точки. Якщо індекс дорівнює нулю, то вважається, що точка розташована зовні многокутника, якщо не нуль, то всередині.

Обчислення індексу відбувається наступним чином. Випускається промінь з заданої точки в довільному напрямку і розглянемо ребра, які він перетинає. Кожному перетинанню приписується число +1 або −1, залежно від того, як ребро перетинає промінь — за годинниковою або проти годинникової стрілки. Сума отриманих величин і є індексом точки.

• Препарата, Франко; Шеймос, Майкл (1985). Computational Geometry – An Introduction. Springer-Verlag. ISBN 0-387-96131-3. 1ша редакція: ISBN 0-387-96131-3; 2ге видання, виправлене і довнене (Розділ 2.2.1).