Мураха Ленгтона

Мураха Ленгтона — двовимірний клітинний автомат з дуже простими правилами, винайдений Крісом Ленгтоном[1]. Мураху можна також вважати двовимірною машиною Тюрінга з 2 символами і 4 станами.[2]

Після 11000 кроків (червоний піксель — місцезнаходження мурахи)

Правила
Перші 200 кроків
Мураха вибирається з квадрату

Розглянемо нескінченну площину, розбиту на клітинки, пофарбовані деяким чином в чорний і білий колір. Нехай в одній з клітин знаходиться «мураха», яка на кожному кроці може рухатися в одному з чотирьох напрямків в клітинку, сусідню по стороні. Мураха рухається згідно з такими правилами:[1][3]

  • На чорному квадраті — повернути на 90° вліво, змінити колір квадрату на білий, зробити крок вперед на наступну клітинку.
  • На білому квадраті — повернути на 90° вправо, змінити колір квадрату на чорний, зробити крок вперед на наступну клітинку.

Ці прості правила викликають досить складну поведінку: після певного періоду досить випадкового руху мураха, мабуть, починає неодмінно будувати дорогу зі 104 кроків, яка повторюється нескінченно, незалежно від початкової розмальовки поля. Це наводить на думку, що «магістральна» поведінка є стабільним атрактором мурахи Ленгтона[1]. Чи є «магістраль» єдиним атрактором при переміщенні мурашки?[4]

Мураха Ленгтона також може бути описана як клітинний автомат, в якому майже все поле пофарбовано в чорно-білий колір, а клітинка з «мурахою» має один з восьми різних кольорів, що кодуює відповідно всі можливі комбінації чорного/білого кольору клітинки і напрямки руху мурахи.

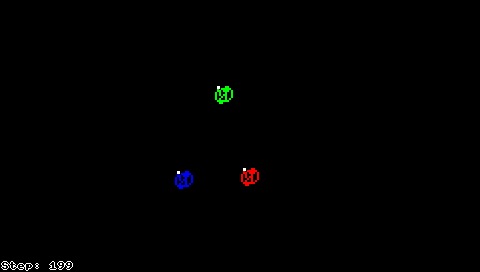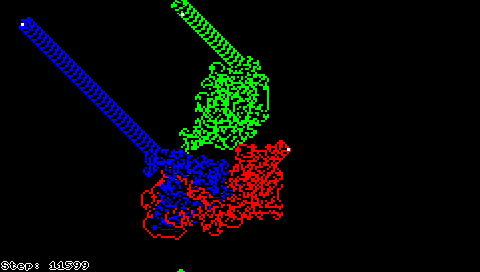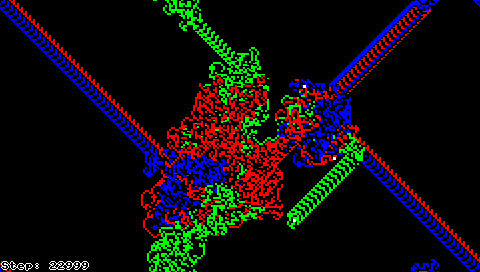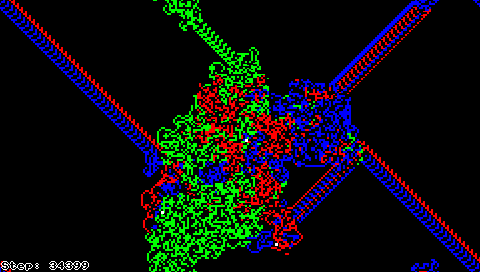
Розширення мурахи Ленгтона

Існує просте розширення мурашки Ленгтона, в якому використовується більше двох кольорів клітинок. Кольори змінюються циклічно. Для таких мурах існує також проста форма назви: для кожного наступного кольору використовується буква L або R (Л і П), в залежності від того, повертає мураха направо, чи наліво. Таким чином, мураха Ленгтона — це мураха RL.

Деякі з цих узагальнених мурах Ленгтона малюють візерунки, які стають все більш симетричними. Один з простих прикладів — мураха RLLR. Одна достатня умова цього полягає в тому, що ім'я мурашки, що розглядається як циклічний список, складається з послідовних пар повторюваних букв LL або RR (циклічність списку означає, що остання буква може об'єднуватися з першою).

  • Приклади:
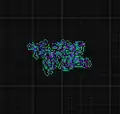  • RLR: Хаотичне зростання
  • LLRR: Симетричне зростання
  • LRRRRRLLR: Заповнює простір в квадраті навколо себе
  • LLRRRLRLRLLR: Створює звивисту магістраль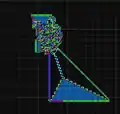
  • RRLLLRLLLRRR
  • L2NNL1L2L1: гексагональне поле, зростання по кільцю
  • L1L2NUL2L1R2: гексагональне поле, спіральне зростання
  • R1R2NUR2R1L2: Анімація

На гексагональному полі існує 6 різних поворотів, які позначені тут як N (без змін), R1 (60° за годинниковою стрілкою), R2 (120° за годинниковою стрілкою), U (180°), L2 (120° проти годинникової стрілки), L1 (60° проти годинникової стрілки).

Тюрміти
  • Приклади:
  • Спіральний ріст
  • Напівхаотичний ріст

Див. також

Примітки
  1. Darling, 2004.
  2. Mária Bieliková, Gerhard Friedrich, Georg Gottlob. SOFSEM 2012: Theory and Practice of Computer Science: 38th Conference on Current Trends in Theory and Practice of Computer Science, Špindlerův Mlýn, Czech Republic, January 21-27, 2012, Proceedings. — Springer, 2012. — P. 394. — ISBN 978-3-642-27660-6.
  3. Стюарт, 2016, с. 411.
  4. Стюарт, 2016, с. 413.

Література
  • David Darling. The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. — John Wiley & Sons, 2004. — P. 180–181. — ISBN 978-0-471-27047-8.
  • Иэн Стюарт. Величайшие математические задачи. — М. : Альпина нон-фикшн, 2016. — 460 с. — ISBN 978-5-91671-507-1.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.