Найменше спільне кратне

Найме́нше спі́льне кра́тне (НСК) двох цілих чисел — найменше натуральне число, яке є кратним обох цих чисел.

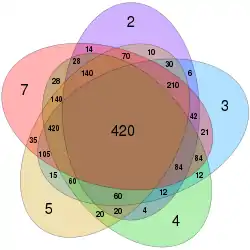
Діаграма Венна зображає найменші спільні кратні для комбінацій із чисел 2, 3, 4, 5 і 7 (6 відсутнє, оскільки 2 × 3, обидва з яких уже представлені).
Наприклад, у грі в карти до 5 гравців, в якій необхідно порівну розділити карти, потребує мати в колоді принаймні 60 карт, це те число, яке є перетином для множин 2, 3, 4, і 5, але не для 7.

Властивості

НСК(a, b) = НСК(b, a) (перестановка аргументів не змінює НСК);

НСК(a, b, c, d) = НСК(НСК(a, b), НСК(c, d));

НСК(a, b) = |ab|/НСД(a, b), де НСД(a, b) — найбільший спільний дільник чисел a, b.

Обчислення НСК методом розкладу на прості множники

Нехай розклад чисел на прості множники

a=2^{q_{2}}\cdot 3^{q_{3}}\cdot \ldots \cdot p_{k}^{q_{p_{k}}};

b=2^{r_{2}}\cdot 3^{r_{3}}\cdot \ldots \cdot p_{k}^{r_{p_{k}}}.

Тоді

НСК

(a,b)=2^{\max(q_{2};r_{2})}\cdot 3^{\max(q_{3};r_{3})}\cdot \dots \cdot p_{k}^{\max(q_{p_{k}};r_{p_{k}})}.

Приклад

Визначимо НСК $(840,396)$ . Розклад на прості множники:

840=2^{3}\cdot 3\cdot 5\cdot 7,

396=2^{2}\cdot 3^{2}\cdot 11;

або, подаючи для наочності нульові степені,

840=2^{3}\cdot 3^{1}\cdot 5^{1}\cdot 7^{1}\cdot 11^{0},

396=2^{2}\cdot 3^{2}\cdot 5^{0}\cdot 7^{0}\cdot 11^{1}.

Отже,

НСК

(840,396)=2^{3}\cdot 3^{2}\cdot 5^{1}\cdot 7^{1}\cdot 11^{1}=27720.

НСК можна теж обчислити за допомогою рівності НСК(a, b) =|ab|/НСД(a, b), використавши для обчислення НСД ефективний алгоритм Евкліда

Реалізація знаходження НСК(lcm) на C++

int lcm(int a, int b)
{
  return (a*b) / gcd(a, b) ;
}

gcd — НСД

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.