Напівсиметричний граф

В області математичної теорії графів, напівсиметричний граф — це неорієнтований граф, який є реберно-транзитивним і регулярним, але не є вершинно-транзитивним. Іншими словами, кожна вершина має однакову кількість інцидентних ребер і є симетрія, яка відображає будь-яке ребро у будь-яке інше, але існує деяка пара вершин таких, що не мають симетрії. Це і є напівсиметричним графом.

Граф Фолкмана — найменший напівсиметричний граф.

Властивості

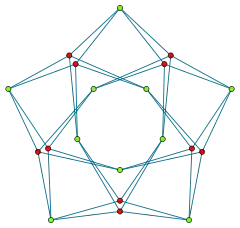
Напівсиметричний граф двочастковий, і його автоморфізм групи повинен діяти транзитивно на кожній з двох поділених вершин. Наприклад, схема графу Фолкмана, яка показана тут. Зелені вершини не можуть бути зівставлені коли червоні будуть автоморфізмами, але кожні дві вершини одного кольору симетричні одна з одною.

Історія

Напівсиметричний граф був вперше досліджений E. Dauber, який був учнем Ф. Харарі, на папері, який вже давно не існує, під назвою «On line- but not point-symmetric graphs». Це зміг помітити  Джон Фолкман який і опублікував цю статтю в 1967 році. Вона включає в себе самий маленький напівсиметричний граф, тепер відомий як граф Фолкмана на 20 вершинах. Термін «напівсиметричний» був вперше використаний і опублікований Кліном у 1978 році.[1]

Кубічні графи

Найменший напівсиметричний кубічний граф (тобто той, в якому кожна вершина має рівно три ребра) — це граф Грея на 54 вершини. Ця напівсиметричність була вперше виявлена Боувером (Bouwer) у 1968 році. А вже довести до розуму найменший кубічний напівсиметричний граф змогли  Dragan Marušič та Aleksander Malnič.[2] Напівсиметричні кубічні графи з 768 вершинами відомі всім. Згідно з Марстоном Кондером, Malnič, Marušič і Potočnik, чотири найменших можливих кубічних напівсиметричних графи після графу Грея є Iofinova–Ivanov граф на 110 вершин,  граф Любляни на 112 вершинах[3], граф на 120 вершин з обхватом 8 та граф 12-клітка Татта.[4]

Примітки
  1. Folkman, J. (1967). Regular line-symmetric graphs. Journal of Combinatorial Theory 3 (3): 215–232. doi:10.1016/S0021-9800(67)80069-3..
  2. Bouwer, I. Z. (1968). An edge but not vertex transitive cubic graph. Bulletin of the Canadian Mathematical Society 11: 533–535. doi:10.4153/CMB-1968-063-0..
  3. Conder, M.; Malnič, A.; Marušič, D.; Pisanski, T.; Potočnik, P. (2002). The Ljubljana Graph. IMFM Preprints (Ljubljana: Institute of Mathematics, Physics and Mechanics) 40 (845)..
  4. Conder, Marston; Malnič, Aleksander; Marušič, Dragan; Potočnik, Primož (2006). A census of semisymmetric cubic graphs on up to 768 vertices. Journal of Algebraic Combinatorics 23 (3): 255–294. doi:10.1007/s10801-006-7397-3..

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.