Олоїд

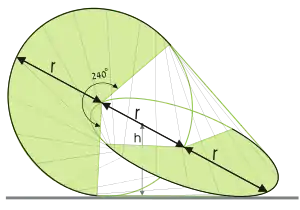
Олоїд — тривимірний криволінійний геометричний об'єкт, відкритий Павлом Шатцем у 1929 році. Це опуклий корпус скелетної рами, зроблений шляхом розміщення двох пов'язаних конгруентних кіл в перпендикулярних площинах, так що центр кожного кола лежить на іншому колі. Відстань між центрами кіл дорівнює радіусу кола. Одна третина периметра кожного кола лежить всередині опуклого корпусу, тому одна і та ж форма може бути сформована як опукла оболонка двох залишкових кругових дуг, кожна з яких охоплює кут 4π / 3.

Структура олоїда. Показано два 240-градусні кругові сектори і опуклий корпус.

Розгортка олоїда

Площа поверхні та об'єм

Площа поверхні олоїда обчислюється за формулою[1]:

A=4\pi r^{2}

,

що дорівнює площі поверхні сфери рівного радіусу.

Об'єм олоїда в кінцевому вигляді обчислюється за формулою[1][2]:

{\frac {2}{3}}\left(2E\left({\frac {3}{4}}\right)+K\left({\frac {3}{4}}\right)\right)r^{3}

,

де K і E означають повні еліптичні інтреграли першого і другого роду відповідно. Чисельний розрахунок дає:

V\approx 3.0524184684r^{3}

Кінетика

Під час кочення кожна точка поверхні олоїда торкається до площини, по якій він котиться[1]. На відміну від більшості аксіально-симетричних об'єктів (циліндр, сфера тощо), при коченні по плоскій поверхні його центр мас рухається по траєкторії меандру, а не лінії. При кожному оберті відстань між центром маси олоїда і поверхнею кочення має два мінімуми і два максимуми. Різниця між максимальною і мінімальною висотою визначається формулою:

\Delta h=r\left({\frac {\sqrt {2}}{2}}-{3}{\frac {\sqrt {3}}{8}}\right)\approx 0.0576r

де r — радіус дуги олоїда. Оскільки ця різниця досить мала, рух олоїда доволі плавний. У кожній точці під час цього руху кочення олоїд дотикається до площини відрізком прямої. Довжина цього відрізка під час руху залишається незмінною і визначається виразом[1][3]:

\!l={\sqrt {3}}r

Пов'язані форми

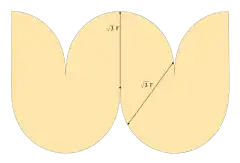
Порівняння олоїда (ліворуч) і сферикона (праворуч) у SVG зображенні. Клацніть на зображенні для перегляду анімації.

Сферикон — опукла оболонка двох півкіл у перпендикулярних площинах з центрами в одній точці. Його поверхня складається з чотирьох шматків конусів. Він схожий на олоїд і, подібно до нього, є поверхнею, що розгортається, яку можна розгорнути шляхом прокочування. Однак його екватор являє собою квадрат, на відміну від екватора олоїда, який кутів не має.

Примітки

Dirnböck, Hans; Stachel, Hellmuth (1997). The development of the oloid. Journal for Geometry and Graphics 1 (2): 105–118. MR 1622664..
OEIS A215447, OEIS A215447
Kuleshov, Alexander S.; Hubbard, Mont; Peterson, Dale L.; Gede, Gilbert (2011). Motion of the Oloid-toy. Proc. 7th European Nonlinear Dynamics Conference, 24–29 July 2011, Rome, Italy. Архів оригіналу за 28 грудня 2013. Процитовано 13 вересня 2017. Архівовано грудень 28, 2013 на сайті Wayback Machine. .

Посилання

Rolling oloid, знято Швейцарським науковим центром Technorama, Вінтертур.
Paper model oloid. Зроби власний олоїд.
Меш олоїда і код для його генерування.
Олоид: математически совершенное произведение искусства. Популярная механика. popmech.ru. Процитовано 13 вересня 2017.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[development-1] Dirnböck, Hans; Stachel, Hellmuth (1997). The development of the oloid. Journal for Geometry and Graphics 1 (2): 105–118. MR 1622664..

[2] OEIS A215447, OEIS A215447

[3] Kuleshov, Alexander S.; Hubbard, Mont; Peterson, Dale L.; Gede, Gilbert (2011). Motion of the Oloid-toy. Proc. 7th European Nonlinear Dynamics Conference, 24–29 July 2011, Rome, Italy. Архів оригіналу за 28 грудня 2013. Процитовано 13 вересня 2017. Архівовано грудень 28, 2013 на сайті Wayback Machine. .