Парадокс Архімеда

Парадо́кс Архіме́да названий на честь відомого Архімеда із Сіракуз, що відкрив славетний закон Архімеда. Парадокс Архімеда можна сформулювати так: «великий корабель може плавати навіть в об'ємі води, що дорівнює декільком склянкам». Цей парадокс випливає з того факту, що для сили Архімеда важливий об'єм зануреної частини тіла, що пливе, а не об'єм води, яка витісняє це тіло.

Тіло може плавати в рідині, маса якої значно менша від маси самого тіла

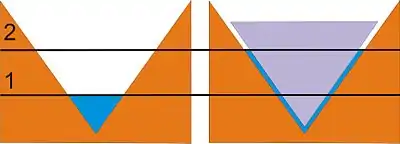
Згідно з законом Архімеда, сила, що діє на тіло, занурене в рідину, дорівнює вазі витісненого ним об'єму рідини. У випадку судна сила Архімеда дорівнює вазі води в об'ємі тієї частини судна, яка занурена у воду. Якщо ця сила більша, ніж вага всього судна, то воно буде плавати.

Парадокс Архімеда можна переформулювати так: тіло може плавати в об'ємі води меншому, ніж об'єм самого тіла, якщо середня густина всього цього тіла менша, ніж густина води, в якій воно плаває. Таким чином, масивне тіло (наприклад, корабель) може плавати в об'ємі води (що залишився) набагато меншому, ніж об'єм самого тіла, за умови, що це тіло взагалі може плавати на широкій поверхні води з такою самою густиною і вода оточує його борти по всій тій поверхні, що й під час звичайного плавання.

Справедливість цього твердження можна продемонструвати таким чином. Візьмемо якесь тіло, що може, не тонучи, плавати на широкій поверхні рідини. Воно зможе плавати і в посудині, габарити якої ненабагато перевищують розміри цього тіла. Потрібно лише підібрати за формою цю посудину так, щоб тіло не торкало її дна та стінок. Можна й далі зменшувати розміри цієї посудини, слідкуючи, щоб між тілом і посудиною завжди залишався якийсь проміжок. Отже, можна теоретично зменшити цей проміжок так, що об'єм води в ньому справді дорівнюватиме лише декільком склянкам, а тіло, як і раніше, буде на плаву.