Параметричне рівняння

Параметричні рівняння — метод представлення математичних функцій через параметри. Простий кінематичний приклад, коли час використовується як параметр для задання позиції, швидкості та іншої інформації про тіло в русі.

Приклад кривої, визначеної параметричними рівняннями — крива метелик.

Параметричне представлення функції

Припустимо, що функціональна залежність y від x не задана прямо y = f(x), а через проміжну величину — t. Тоді формули

x=\varphi (t)~;~

~y=\psi (t)

задають параметричні рівняння для функції однієї змінної.

Якщо припустити, що обидві ці функції $\varphi$ і $\psi$ мають похідні і для $\varphi$ існує обернена функція θ, явне представлення функції має вигляд[1]:

~y=\psi (\theta (x))=f(x)

і похідна функції може бути обрахована як

y'(x)={\frac {dy}{dx}}={\frac {y'_{t}}{x'_{t}}}={\frac {\psi '(t)}{\phi '(t)}}

2D-приклади

Парабола

Тривіальний приклад, рівняння параболи:

y=x^{2}\,

може бути параметризоване із використанням параметра t таким чином

x=t\,

y=t^{2}.\,

Коло

Для кола радіуса a:

x=a\cos(t)\,

y=a\sin(t).\,

3D-приклади

Гвинтова лінія

Параметризована гвинтова лінія

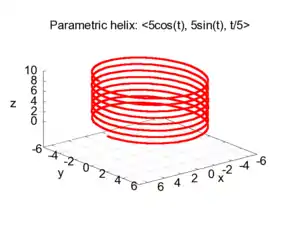
Параметричні рівняння зручні для опису кривих і в багатовимірних просторах. Наприклад:

x=a\cos(t)\,

y=a\sin(t)\,

z=bt\,

описує тривимірну криву, гвинтова лінія, яка має радіус a і підіймається на 2πb за оберт.

Подібні вирази також записуються як

r(t)=(x(t),y(t),z(t))=(a\cos(t),a\sin(t),bt).\,

Корисність

Такий спосіб представлення є практичним і ефективним; наприклад, можна інтегрувати і брати похідну почленно. Таким чином, швидкість точки, що рухається згідно з цими рівняннями може бути представлена як:

v(t)=r'(t)=(x'(t),y'(t),z'(t))=(-a\sin(t),a\cos(t),b)\,

і прискорення:

a(t)=r''(t)=(x''(t),y''(t),z''(t))=(-a\cos(t),-a\sin(t),0)\,

Загалом, параметризована крива є функцією від одного параметра (зазвичай t). Для відповідного випадку із двома і більше параметрами, дивись параметрична поверхня.

Примітки

Г. М. Фіхтенгольц. «Курс диференціального та інтегрального числення». Том I. Москва 1969 г. Стор. 218

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Ref189-1] Г. М. Фіхтенгольц. «Курс диференціального та інтегрального числення». Том I. Москва 1969 г. Стор. 218