Поризм Штейнера

Поризм Штейнера: Розглянемо ланцюжок кіл ${\displaystyle S_{1},S_{2},\ldots ,S_{n}}$, кожне з яких дотикається до двох сусідніх (${\displaystyle S_{n}}$ дотикається до ${\displaystyle S_{n+1}}$ і ${\displaystyle S_{n-1}}$) і двох даних неперетинних кіл ${\displaystyle R_{1}}$ і ${\displaystyle R_{2}}$. Тоді для будь-якого кола ${\displaystyle T_{1}}$, яке дотикається до ${\displaystyle R_{1}}$ і ${\displaystyle R_{2}}$ (однаковим чином, якщо ${\displaystyle R_{1}}$ і ${\displaystyle R_{2}}$ не лежать одна в іншій, зовнішнім і внутрішнім чином — в іншому випадку), існує аналогічний ланцюжок з ${\displaystyle n}$ дотичних кіл ${\displaystyle T_{1},T_{2},\ldots ,T_{n}}$.

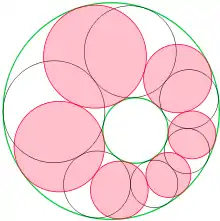
Див. також анімований варіант

Доводиться застосуванням інверсії, яка переводить пару кіл ${\displaystyle R_{1}}$ і ${\displaystyle R_{2}}$ в концентричні.