Ланцюг Паппа Александрійського
Ланцюг Паппа Александрійського — кільце всередині двох дотичних кругів, заповнених попарно дотичними кругами менших діаметрів. Досліджена Паппом Александрійським у III столітті н. е.
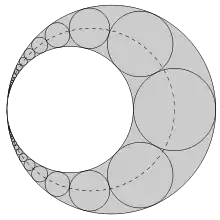
Побудова
Беремо точки у такому порядку на одній прямій та побудуємо кола та з діаметрами та відповідно, центри яких позначимо та . Фігура, обмежена колами, схожа з арбелосом (але складається з двох дуг окружності замість трьох) та допускає ланцюг кіл, так як і у теоремі Паппа Александрійського. При цьому кожне коло з ланцюга дотикається окружності ззовні, окружності зсередини та двох сусідніх кіл ланцюга.
Властивості
- Центри кіл ланцюга розташовані на спільному еліпсі, фокусами якого є центри и кіл яка охоплює фігури, оскільки сума відстаней від центру n-го до точок та не залежить від n:
- Якщо , то центр та радіус n-го кола ланцюга задаються формулами
Інверсія кола
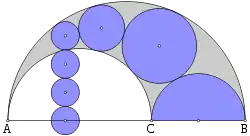
Висота hn центру n-го кола над основним діаметром ACB дорівнює n помножене на dn.[1] Це може бути показано за допомогою інверсії відносно кола з центром у дотичній точці A. Інверсія кола обирається таким чином, щоб перетнути n-те коло перпендикулярно, так щоб n-те коло відображалось само на себе. Два орбелосних кола, та , перетворюються на паралельні лінії, що дотичні до зміщеного n-го кола; отже, інші кола ланцюга Паппа перетворюються на аналогічно затиснуті кола одного діаметру. Початкове коло та кінцеве коло , кожне додають ½dn до висоти hn, тоді як кола C1–Cn−1, кожне додає dn. Сума цих висот дає рівняння hn = n dn.
Таку ж інверсію можна використати для того, щоб показати, що точки де кола ланцюга Паппа дотичні один до одного лежать на спільному колі. Як показано вище, інверсія відносно точки A перетворює арбелосні кола та на дві паралельні лінії, а кола ланцюга Паппа на купу рівних кіл затиснутих між двома паралельними лініями. Отже, точки дотику між перетвореними колами лежить на середині лінії між двома паралельними лініями. Обертаючи інверсію в колі, ця лінія дотичних точок перетворюється назад у коло.
Ланцюг Штейнера
У цих властивостях, що мають центри на еліпсі та точки дотику на колі, ланцюг Паппа аналогічний ланцюгу Штайнера, в якому скінченне число кіл дотикаються до двох кіл.
Примітки
- Ogilvy, pp. 54–55.
Література
- Ogilvy, C. S. (1990). Excursions in Geometry. Dover. с. 54–55. ISBN 0-486-26530-7.
- Bankoff, L. (1981). How did Pappus do it?. У Klarner, D. A. The Mathematical Gardner. Boston: Prindle, Weber, & Schmidt. с. 112–118.
- Johnson, R. A. (1960). Advanced Euclidean Geometry: An elementary treatise on the geometry of the triangle and the circle (вид. reprint of 1929 edition by Houghton Miflin). New York: Dover Publications. с. 116–117. ISBN 978-0-486-46237-0.
- Wells, D. (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. с. 5–6. ISBN 0-14-011813-6.
Посилання
- Floer van Lamoen and Eric W. Weisstein Pappus Chain(англ.) на сайті Wolfram MathWorld.
- Tan, Stephen. Arbelos.