Потужність джерела звуку

Процес поширення звуку не пов'язаний з поступальним рухом частинок середовища. В цьому процесі визначальним є перенос стану збурення від області його зародження по всьому об'єму, який займає акустичне середовище. Такий перенос це, по суті, перенос енергії збурення і тому енергетичні характеристики звукового поля і джерела звуку є важливими при аналізі процесів генерації та поширення звуку. Загальні властивості енергетики процесу випромінювання звуку і зміст понять, що використовуються для його описання проілюстровано на прикладі простого сферичного джерела. ЦІ результати важливі для розуміння енергетики генерації звуку джерелами різних форм.

Випромінювання звуку сферичним джерелом

Взаємодія стисливого середовища з будь-яким тілом, поверхня якого коливається, є одним із основних механізмів генерації звуку. У випадку, коли тіло є сферою, відносно проста математична модель процесу дає можливість розкрити зміст основних понять, що характеризують випромінювання. При аналізі хвильових процесів часто використовують представлення збурень у вигляді суперпозиції періодичних (гармонічних) збурень. Детальний аналіз задачі про випромінювання таких збурень сферою, що пульсує, проведено в[1]. Тут використано представлені в посібнику розв'язки. Рис. 1 показує переріз сфери і сферичні координати, що використовуються при математичному моделюванні акустичних процесів. В цьому випадку мова йде про випромінювання звуку сферою, на поверхні якої задано рівномірно розподілену коливальну швидкість з частотою $\omega$ .

Рис.1 Геометрія сфери. Сферичні координати.

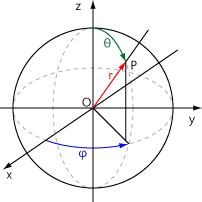
Для зручності гранична умова на поверхні сфери радіуса $R=a$ записується з використанням комплексної експоненти в вигляді $V_{r}(r=a)=V_{0}exp(-i\omega t)$ . Зручність такого запису проявляється в тому, що тепер легко записати вирази для коливальної швидкості частинок середовища та тиску з урахуванням вимоги випромінювання звуку на нескінченності.

$v_{r}(r,t)=-{\frac {1}{i\omega \rho }}({\frac {1}{r^{2}}}-{\frac {ik}{r}})Aexp(-i\omega t+ikr),$ ,

$p(r,t)={\frac {A}{r}}exp(-i\omega t+ikr),$

$A=-i\omega \rho {\frac {V_{0}a^{2}}{1-ika}}exp(-ika),k={\frac {\omega }{c}}={\frac {2\pi }{\lambda }}$

В цих виразах $k$ - хвильове число, $c$ -швидкість звуку, $\lambda$ -довжина хвилі. Вимога умови випромінювання врахована вибором знаків складових в показнику експоненти. Різні знаки між часовою та просторовою складовими вказує на те, що фазова швидкість хвилі направлена в сторону зростання величини радіуса.

Потік енергії в сферичній хвилі

Потік енергії в хвильових процесах різної фізичної природи визначається вектором Умова — Пойнтінга. Для даної задачі маємо єдину радіальну компоненту цього вектора. Для обчислення величини потоку енергії слід використовувати лише дійсні частини в виразах для швидкості та тиску. Потік енергії існує в будь-якій точці поза сферою і обчислюється за формулою $I(r,t)=RepRev$ . Ця формула є просто частинним випадком загального співвідношення для визначення потужності в механіці. Не можна прямо використовувати комплексне представлення характеристик звукового поля при обчисленнях оскільки потужність є нелінійною його характеристикою. В цьому випадку задача випромінювання звуку сферою розглядається в рамках моделі ідеальної рідини, в якій відсутні втрати енергії хвилі при її поширенні. Тому загальну оцінку випроміненої потужності можна одержати інтегруванням величини потоку енергії по поверхні сфери будь-якого радіуса. З метою ілюстрації ролі розмірів випромінювача здійснимо таке обчислення інтегралу по поверхні випромінювача.

Енергія випромінювання сферичним джерелом

Виділяючи дійсні частини в одержаних загальних виразах для коливальної швидкості та тиску для миттєвого потоку енергії з одиниці поверхні сфери (інтенсивність звуку) одержимо наступний вираз

$I(\omega t)=\rho cV_{0}^{2}\left[{\frac {(ka)^{2}}{1+(ka)^{2}}}cos^{2}(\omega t)+{\frac {ka}{1+(ka)^{2}}}sin(\omega t)cos(\omega t)\right](1)$

Цей вираз в певному сенсі типовий для будь якого по формі скінченного джерела звуку. Для нього завжди миттєвий потік енергії буде мати дві принципово різні складові. Перша складова цього виразу має множником $cos^{2}(\omega t)$ . Цей множник завжди додатний і, відповідно, потік енергії завжди спрямований на нескінченність. Що стосується другого доданку то він змінює знак кожні пів періода $T={\frac {2\pi }{\omega }}$ . Пів періоду енергія перетікає від випромінювача до акустичного середовища, а пів періоду повертається назад до випромінювача. Ця різниця в поведінці складових потоку енергії в звуковому полі, що генерується скінченним за розмірами джерелом, знаходить відображення в термінології. Першу складову називають активним потоком енергії, а другу — реактивним потоком[2]. Така структура виразу для миттєвої потужності випромінювання відображає загальну властивість процесів випромінювання енергії скінченним за розмірами джерелом для хвиль різної фізичної природи. Загальна потужність випромінювання за одиницю часу в цьому випадку обчислюється за простою формулою $w=4\pi a^{2}I(\omega t)$ .

Формулою (1) представлено щільність потоку енергії, що випромінюється джерелом, на одній частоті. Як правило, в практиці використовуються джерела, що випромінюють звук в певному частотному діапазоні. При обчисленні енергії випромінювання в цьому випадку слід мати на увазі, що енергія звукового поля є квадратичною функцією його характеристик- швидкості частинок і тиску. Тому для оцінки потоку енергії не можна використовувати принцип суперпозиції. Характер поправки до принципу суперпозиції видно на прикладі звукового поля, що складається з двох плоских хвиль. В цьому випадку для обчислення миттєвої щільності потоку енергії слід використовувати формулу[1].

I={\frac {p^{2}}{\rho c^{2}}}

Якщо звукове поле утворено двома пласкими хвилями

p_{1}=acos(k_{1}x-\omega _{1}t),p_{2}=bcos(k_{2}x-\omega _{2}t)

щільність потоку енергії в ньому визначається формулою

I=I_{1}+I_{2}+{\frac {2ab}{\rho c^{2}}}cos(k_{1}x-\omega _{1}t)cos(k_{2}x-\omega _{2}t).(2)

Тут $I_{1}$ та $I_{2}$ відповідно потоки енергії в першій та другій хвилі окремо. Третій доданок описує додатковий потік енергії, що виникає в результаті взаємодії між хвилями. Принцип суперпозиції для потоків енергії має місце лише для пласких хвиль, що поширюються на зустріч одна одній[3].

В багатьох практично цікавих випадках визначальною характеристикою джерела звуку є не миттєве значення потоку енергії, а величина випромінюваної енергії за характерний проміжок часу. Стосовно гармонічних хвиль це може бути період коливань, а для широкосмугових сигналів це відрізок часу, що суттєво перевищує період коливань складової з найменшою частотою. При такому усередненні по часу зникає реактивна складова в виразі (1) та третій доданок в формулі (2).

Залежність характеристик від хвильового розміру джерела

Фізичні особливості процесу випромінювання звуку розкриваються при більш детальному аналізі загальної формули (1). Перш за все слід звернути увагу на те, що реальні фізичні розміри випромінювача в цю формулу не входять. Єдиною характеристикою випромінювача є величина $ka$ , що визначається співвідношенням радіуса сфери та довжини хвилі. Тому в загальному випадку при аналізі випромінювання звуку визначальною величиною для характеристики випромінювача є його хвильовий розмір коли масштабом для характеристики випромінювача є не метр чи сантиметр, а довжина хвилі. Оскільки витрати енергії на створення реактивного потоку потужності є небажаними важливо оцінити залежність величини потоків активної і реактивної енергії. Наочне зображення співвідношення цих величин у відповідності до формули (1) представлено на рис.2. Тут в логаритмічному масштабі зображено залежності від хвильового розміру випромінювача першого (активна потужність) і другого коефіцієнту (реактивна потужність) в квадратних дужках в виразі (1). Значення цих коефіцієнтів представлено в децибелах. При цьому в якості опорного значення величин вибрано одиницю. Видно, що співвідношення між небажаною реактивною та корисною активною складових в потоці акустичної енергії суттєво залежить від хвильових розмірів випромінювача. При малих його хвильових розмірах реактивна складова може в сотні разів перевищувати активну складову.

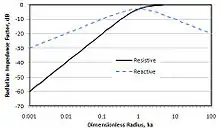
Рис.2. Співвідношення активної і реактивної потужності при різних хвильових розмірах випромінювача.

Тому збільшення хвильових розмірів випромінювача є очевидною рекомендацією для підвищення ефективності випромінюючих звук пристроїв. Однак практично цю рекомендацію часто неможливо реалізувати.

Загальній аналіз виразів для характеристик звукового поля створеного пульсуючою сферою дозволяє більш глибоко проаналізувати особливості процесу випромінювання звуку. Якщо проаналізувати процес одержання загальної формули (1) для щільності потоку потужності, то можна бачити, що поява реактивної складової в загальному потоці пов'язане з наявністю складової в виразі для коливальної швидкості частинок середовища обернено пропорційної квадрату відстані від поверхні випромінювача. Такі збурення досить швидко зменшуються при віддаленні від поверхні випромінювача. Ця обставина відображається введенням в акустиці терміну ближнє поле випромінювача. Реактивна потужність витрачається на створення цього поля. Відповідно, на великій відстані від випромінювача (в дальньому полі) визначальним є внесок активної складової потоку енергії.

Приклади випромінювачів та характерні величини енергії звукових полів

Рис.3. Для ефективної передачі звуків різних частот використовується система випромінювачів з різними хвилевими розмірами. 1 — випромінювач середніх частот загального частотного діапазону, 2 — випромінювач високих частот і 3 — випромінювачі низьких частот.

Характеризуючи енергетичні аспекти процесу генерації звуку доцільно привести конкретні значення величин енергії, що накопичується в звуковому полі в різних реальних ситуаціях.

Кількісно енергетика більшості звукових процесів характеризується дуже малими (в «побутових» масштабах) величинами навіть для дуже гучних звуків. Так під час нормальної розмови між людьми на відстані 1 метра від того, хто говорить, в повітрі накопичується енергія збурення в $1.4\cdot 10^{-8}{\frac {erg}{sm^{3}}}$ . Для порівняння можна вказати, що у великій концертній залі з об'ємом 20000 кубічних метрів при фортисимо оркестру повна накопичена звукова енергія досягає $10^{6}erg$ . Цієї енергії (густина якої на чотири порядки вища ніж при розмові) достатньо лише для того, щоб виконати роботу по підйому в полі земного тяжіння вантажу в 10 г на висоту 1 м. Крім всього іншого ці дані вказують на надзвичайну чутливість людського вуха. Так, в області частот 2000-3000 Гц, де людське вухо найбільш чутливе, найслабші збурення, які людина ще сприймає як звук пов'язані з коливанням частинок середовища зі швидкістю 2 м за рік[3]. Людське вухо характеризується не лише винятковою чутливістю до незначних збурень. Важливою також є його здатність сприймати збурення як звук в надзвичайно широкому діапазоні зміни енергії звуку. Природні явища, робота машин і механізмів, створених людиною, супроводжуються генерацією звуків різного енергетичного рівня. Інформація про певні характерні звуки широко представлена в наступному довіднику[4]. Представлено дані в діапазоні від найпотужнішого джерела — ракетного комплексу, що забезпечив політ астронавтів на Луну ( $10^{8}$ Вт), до найслабшого звуку, що генерується людиною при диханні ( $10^{-11}$ Вт).

Суттєва залежність ефективності випромінювання звуку (активна складова потоку енергії) від хвильового розміру випромінювача є об'єктивною фізичною причиною виникнення труднощів при створенні акустичних систем, призначених для відтворення широкосмугових звукових сигналів. Аналіз різних аспектів цієї інженерної проблеми та та розробка конкретних рекомендацій для створення систем для конкретних умов використання є предметом такого розділу акустики, як електроакустика[5][6]. Одним із способів підвищення акустичної якості гучномовців є використання систем випромінювання з декількома випромінювачами, призначеними для роботи в різних частотних діапазонах. Конкретний пристрій, впри створенні якого використана ця ідея, показано на рис.3.

Див. також

Примітки

Грінченко В. Т., Вовк І. В., Маципура І. Т. Основи акустики , Київ.: Наукова думка, 2007, — 640 с.
Sound Power Level.
Исакович М. А.Общая акустика, Москва, Наука, 1073, -496 с.
The Engineering TollBox
Кононов С. П. Основи звукотехніки
Ferris, R. H. (15 вересня 1965). Tests of the Project Artemis Acoustic Source. Washington, D.C.: U.S. Naval Research Laboratory.

Література

Римский-Корсаков А. В. Электроакустика,Москва, Связь, 1973, -272 с.
Kleiner M. Electroacoustics, CRC Press, 2013, -585 c.
Алдошина И. А., Вологдин В. И., Ефимов А. П. и др. Электроакустика и звуковое вещание: Учебное пособие для вузов. Москва, Радио и связь, 2007. -872 с.
Фурдуев В. В. Электроакустика, Гостехиздат, Москва-Ленинград, 1948. -515 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[hrinchenko1-1] Грінченко В. Т., Вовк І. В., Маципура І. Т. Основи акустики , Київ.: Наукова думка, 2007, — 640 с.

[2] Sound Power Level.

[isakovich-3] Исакович М. А.Общая акустика, Москва, Наука, 1073, -496 с.

[4] The Engineering TollBox

[5] Кононов С. П. Основи звукотехніки

[6] Ferris, R. H. (15 вересня 1965). Tests of the Project Artemis Acoustic Source. Washington, D.C.: U.S. Naval Research Laboratory.