Правильний сімнадцятикутник
Правильний сімнадцятикутник — геометрична фігура, що належить до групи правильних многокутників. Має сімнадцять сторін і сімнадцять кутів. Усі кути і сторони правильного сімнадцятикутника рівні між собою, всі вершини лежать на одному колі.

Властивості
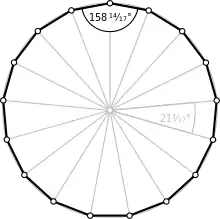
Центральний кут α дорівнює .
Відношення довжини сторони до радіусу описаного кола складає
- .
Правильний сімнадцятикутник можна побудувати за допомогою циркуля та лінійки, що було доведено Карлом Фрідріхом Гаусом 1796 року. Ним же знайдено значення косинуса центрального кута сімнадцятикутника:
.
Факти
- Гаус був настільки піднесений своїм відкриттям, що в кінці життя заповів, щоб правильний сімнадцятикутник викарбували на його могилі. Скульптор відмовився це зробити, стверджуючи, що побудова буде настільки складною, що результат не можна буде відрізнити від кола[1].
- 1825 року Йоханес Ерхінгер уперше опублікував детальний опис побудови правильного сімнадцятикутника за 64 кроки. Нижче наводиться ця побудова.
Побудова
Точна побудова
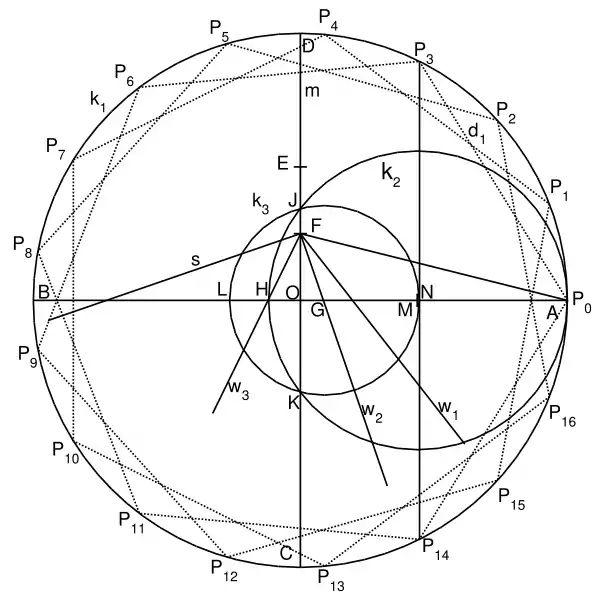
- Проводимо велике коло k₁ (майбутнє описане коло сімнадцятикутника) з центром O.
- Проводимо його діаметр AB.
- Будуємо до нього перпендикуляр m, перетинаючий k₁ у точках C та D.
- Відмічаємо точку E — середину DO.
- Посередині EO відмічаємо точку F та проводимо відрізок FA.
- Будуємо бісектрису w₁ кута ∠OFA.
- Будуємо w₂ — бісектрису кута між m та w₁, яка перетинає AB у точці G.
- Проводимио s — перпендикуляр до w₂ з точки F.
- Будуємо w₃ — бісектрису кута між s та w₂. Вона перетинає AB у точці H.
- Будуємо коло Фалеса (k₂) на діаметрі HA. Воно перетинається з CD у точках J та K.
- Проводимо коло k₃ з центром G через точки J та K. Воно перетинається з AB у точках L та N. Тут важливо не переплутати N з M, вони розташовані дуже близько.
- Будуємо дотичну до k₃ через N.
Точки перетину цієї дотичної до вихідного кола k₁ — це точки P₃ та P₁₄ шуканого сімнадцятикутника. Якщо прийняти середину отриманої дуги за P₀ та відкласти дугу P₀P₁₄ по колу тричі, усі вершини сімнадцятикутника будуть побудовані.
Приблизна побудова
Наступна побудова хоч і наближена, але набагато зручніша.
- Ставимо на площині точку M, будуємо навколо неї коло k та проводимо її діаметр AB;
- Ділимо навпіл радіус AM тричі по черзі в напрямку до центру (точки C, D та E).
- Ділимо навпіл відрізок EB (точка F).
- Будуємо перпендикуляр до AB у точці F.
- Коротко: будуємо перпендикуляр до діаметра на відстані 9/16 діаметра від B.
Точки перетину останнього перпендикуляра перпендикуляра з колом ї гарним наближенням для точок P₃ та P₁₄.
При цій побудові виходить відносна похибка у 0,83 %. Кути та сторони виходять таким чином трохи більші, ніж потрібно. При радіусі 332,4 мм сторона виходить довшою на 1 мм.
Анімована побудова Ерхінгера

Примітки
Посилання
- Karin Reich: Die Entdeckung und frühe Rezeption der Konstruierbarkeit des regelmäßigen 17-Ecks und dessen geometrische Konstruktion durch Johannes Erchinger (1825). В кн.: Mathesis, Festschrift zum siebzigsten Geburtstag von Matthias Schramm. Hrsg. von Rüdiger Thiele, Berlin, Diepholz 2000, стр. 101–118.