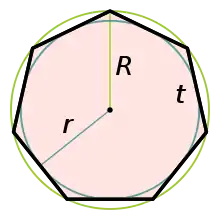
Правильний многокутник

Нехай ${\displaystyle x_{0}}$ та ${\displaystyle y_{0}}$ — координати центра, а ${\displaystyle R}$ — радіус описаного навколо правильного многокутника кола, ${\displaystyle {\phi }_{0}}$ — кутова координата першої вершини, тоді декартові координати вершин правильного многокутника визначаються формулами

${\displaystyle x_{i}=x_{0}+R\cos \left({\phi }_{0}+{\frac {2\pi i}{n}}\right)}$,

${\displaystyle y_{i}=y_{0}+R\sin \left({\phi }_{0}+{\frac {2\pi i}{n}}\right)}$,

де ${\displaystyle i=0,\dots ,n-1}$.

Нехай ${\displaystyle R}$ — радіус описаного навколо правильного многокутника кола; тоді радіус вписаного кола дорівнює

${\displaystyle r=R\cos {\frac {\pi }{n}}}$,

а довжина сторони многокутника рівна

${\displaystyle t=2R\sin {\frac {\pi }{n}}}$.

Площа правильного многокутника з числом сторін ${\displaystyle n}$ та довжиною сторони ${\displaystyle t}$ обчислюється за формулою

${\displaystyle S={\frac {n}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{n}}}$.

Площа правильного многокутника з числом сторін ${\displaystyle n}$, вписаного в коло радіусу ${\displaystyle R}$ обчислюється за формулою

${\displaystyle S={\frac {n}{2}}R^{2}\sin {\frac {2\pi }{n}}}$.

Площа правильного многокутника з числом сторін ${\displaystyle n}$, описаного навколо кола радіусу ${\displaystyle r}$ обчислюється за формулою

${\displaystyle S=nr^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{n}}}$ (площа основи n-кутної правильної призми)

Правильний многокутник може бути розкладеним на стільки рівних рівнобічних трикутників, скільки в нього є сторін. Кожний із трикутників має за основу сторону многокутника, а як висоту — апофему. Досить згадати, як знаходять площу трикутника, тобто

${\displaystyle S={\frac {1}{2}}bh,}$

де S — площа, b — основа, h — висота. Отже, площа правильного многокутника обчислюється за формулою:

${\displaystyle S={\frac {1}{2}}lan={\frac {1}{2}}pa}$

де l — сторона, a — апофема, n — кількість сторін, p — периметр.

Обернені формули:

${\displaystyle p={\frac {2S}{a}}}$
${\displaystyle a={\frac {2S}{p}}}$

Щоб полегшити ситуацію, для кожного правильного многокутника знайшли відношення між апофемою і стороною. Для правильного трикутника таке відношення становить ~0,29, для квадрата — 0,5, для правильного п'ятикутника — ~0,69, для шестикутника — ~0,87 і т. д.