Правильний ікосаедр
Правильний ікоса́едр (від грец. εικοσάς, «двадцять» і грец. —εδρον, «грань», «лице», «основа») — правильний опуклий многогранник, двадцятигранник, одне з Платонових тіл. Кожна з 20 граней є рівностороннім трикутником. Число ребер рівне 30, число вершин — 12.
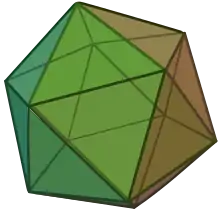
Ікосаедр, натисніть тут для обертання моделі

Тривимірна модель правильного ікосаедра
Формули
Площа S, об'єм V ікосаедра з довжиною ребра a, а також радіуси вписаної і описаної куль обчислюються за формулами:
;
;
;
.
Декартові координати
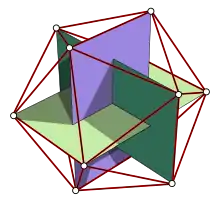
Золоті прямокутники в ікосаедрі
Вершини ікосаедра з довжиною ребра 2 і центром в початку координат визначають такі декартові координати:
- (0, ±1, ±φ);
- (±1, ±φ, 0);
- (±φ, 0, ±1),
де φ = (1+√5)/2 є «золотим перетином». Зауважте, що ці набори вершин формують взаємно відцентровані і взаємно ортогональні золоті прямокутники.
Властивості
- Ікосаедр можна вписати в куб, при цьому його шість взаємно паралельних ребер розташовуватимуться відповідно на шести гранях куба, решта 24 ребра - усередині куба, а усі дванадцять вершин ікосаедра лежатимуть на шести гранях куба.
- В ікосаедр може бути вписаний тетраедр, притому чотири вершини тетраедра будуть суміщені з чотирма вершинами ікосаедра.
- Ікосаедр можна вписати в додекаедр, притому вершини ікосаедра будуть суміщені з центрами граней додекаедра.
- У ікосаедр можна вписати додекаедр, притому вершини додекаедра будуть суміщені з центрами граней ікосаедра.
У фізичному світі

Розгортка ікосаедра
- Капсиди багатьох вірусів (наприклад, бактеріофаги, мімівірус).
Посилання
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Paper Models of Polyhedra Many links
- Origami Polyhedra — Models made with Modular Origami
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.