Процес Грама — Шмідта

Перші 2 кроки ортогоналізації

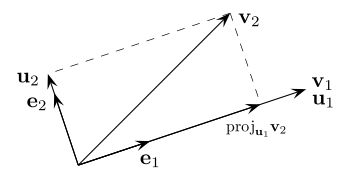
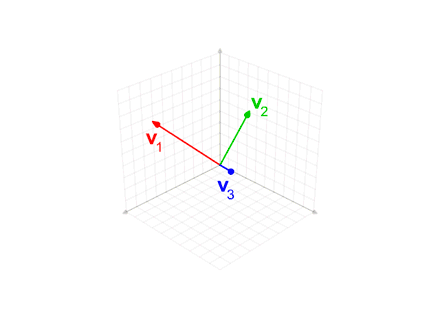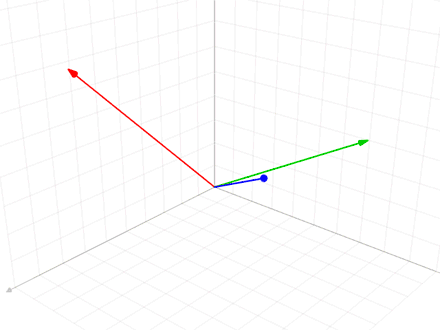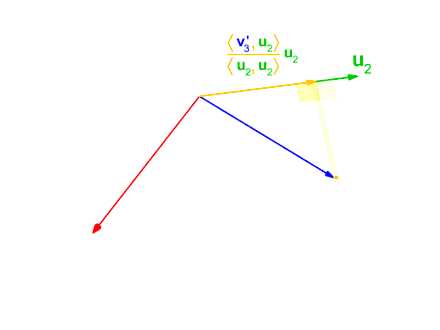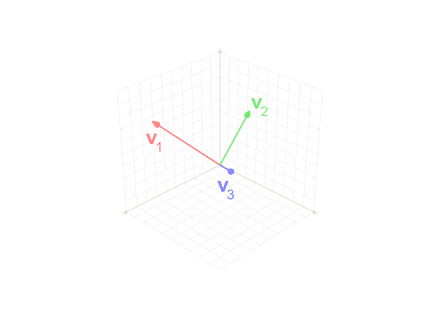
Визначимо ортогонально-проекційний оператор

${\displaystyle \mathrm {proj} _{\mathbf {u} }\,\mathbf {v} ={\langle \mathbf {u,v} \rangle \over \langle \mathbf {u,u} \rangle }\mathbf {u} ={\mathbf {uu^{\top }} \over \langle \mathbf {u,u} \rangle }\cdot \mathbf {v} =\mathbf {ee^{\top }} \cdot \mathbf {v} ,\qquad \mathbf {e} ={\mathbf {u} \over \|\mathbf {u} \|},}$

де <u, v> означає скалярний добуток векторів u and v. Цей оператор проектує вектор v ортогонально на вектор u.

Приймемо ${\displaystyle \mathbf {u} _{1}=\mathbf {v} _{1}}$ та запишемо рекурсивну формулу

${\displaystyle \mathbf {u} _{i}=\mathbf {v} _{i}-\sum _{j=1}^{i-1}{\frac {\langle \mathbf {v} _{i},\mathbf {u} _{j}\rangle }{\langle \mathbf {u} _{j},\mathbf {u} _{j}\rangle }}\mathbf {u} _{j}=\mathbf {v} _{i}-{\bigg (}\sum _{j=1}^{i-1}\mathbf {e} _{j}\mathbf {e} _{j}^{\top }{\bigg )}\mathbf {v} _{i}.}$

Нормуючи вектори ${\displaystyle \mathbf {u} _{i}}$, отримаємо ортонормовану систему о${\displaystyle \{\mathbf {e} _{i}\}}$.

Геометричний зміст процесу в тому, що вектор ${\displaystyle \mathbf {u} _{i}}$ є проекцією вектора ${\displaystyle \mathbf {v} _{i}}$ на перпендикуляр до лінійної оболонки векторів ${\displaystyle \mathbf {v} _{1},\dots ,\mathbf {v} _{i-1}.}$

• Для кожного ${\displaystyle \ i}$ лінійні оболонки систем ${\displaystyle \mathbf {v} _{1},\dots ,\mathbf {v} _{i}}$ та ${\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{i}}$ збігаються.
• Добуток довжин ${\displaystyle \mathbf {u} _{i}}$ дорівнює об'єму паралелепіпеда, побудованого на векторах системи ${\displaystyle \{\mathbf {v} _{i}\}}$, як на ребрах.

Коли процес втілено на комп'ютері, вектори ${\displaystyle \mathbf {u} _{k}}$ часто не точно ортогональні, через похибки заокруглювання. Для процесу Грама — Шмідта у вигляді описаному вище (іноді згадуваному як «класичний Грам — Шмідт») ця втрата ортогональності особливо шкідлива; кажуть, що (класичний) процес Грама — Шмідта числово нестійкий.

Процес Грама — Шмідта можна стабілізувати завдяки маленькій зміні; цю версію іноді згадують як модифікований Грам — Шмідт. Цей підхід дає той самий результат що й оригінальна формула в точній арифметиці і вводить менші похибки в арифметиці скінченної точності. Замість того, щоб обчислювати вектор u_k як

${\displaystyle \mathbf {u} _{k}=\mathbf {v} _{k}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{k})-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {v} _{k})-\cdots -\mathrm {proj} _{\mathbf {u} _{k-1}}\,(\mathbf {v} _{k}),}$

його обчислюють як

${\displaystyle {\begin{aligned}\mathbf {u} _{k}^{(1)}&=\mathbf {v} _{k}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{k}),\\\mathbf {u} _{k}^{(2)}&=\mathbf {u} _{k}^{(1)}-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {u} _{k}^{(1)}),\\&\,\,\,\vdots \\\mathbf {u} _{k}^{(k-2)}&=\mathbf {u} _{k}^{(k-3)}-\mathrm {proj} _{\mathbf {u} _{k-2}}\,(\mathbf {u} _{k}^{(k-3)}),\\\mathbf {u} _{k}^{(k-1)}&=\mathbf {u} _{k}^{(k-2)}-\mathrm {proj} _{\mathbf {u} _{k-1}}\,(\mathbf {u} _{k}^{(k-2)}).\end{aligned}}}$

Кожен крок знаходить вектор ${\displaystyle \mathbf {u} _{k}^{(i)}}$ ортогональний до ${\displaystyle \mathbf {u} _{k}^{(i-1)}}$. Таким чином, ${\displaystyle \mathbf {u} _{k}^{(i)}}$ також ортогональний похибкам введеним під час обчислення ${\displaystyle \mathbf {u} _{k}^{(i-1)}}$.

• Гантмахер Ф. Р. Теория матриц. — 2 изд. — Москва : Наука, 1967. — 576 с. — ISBN 5-9221-0524-8.(рос.)
• Гельфанд И. М. Лекции по линейной алгебре. — 5-е. — Москва : Наука, 1998. — 320 с. — ISBN 5791300158.(рос.)