Паралелепіпед

Паралелепі́пед (від грец. παράλλος — паралельний і επιπεδον — площина) — призма, основою для якої є паралелограм.[1][2]

Властивості

Всі 6 граней паралелепіпеда є паралелограмами.[3]
Протилежні грані рівні та паралельні.[4]
Діагоналі перетинаються в одній точці та діляться в ній навпіл.[4]

Типи паралелепіпедів

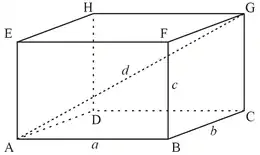
Прямокутний паралелепіпед і його виміри a, b, c

Розрізняють декілька типів паралелепіпедів:

Прямий паралелепіпед — паралелепіпед, бічні ребра якого перпендикулярні до площини основи.[1] У прямих паралелепіпедів чотири грані є прямокутниками, а основи — паралелограмами.[3] Паралелепіпеди, які не є прямими, називаються похилими.
Прямокутний паралелепіпед — прямий паралелепіпед, основою в якому є прямокутник.[3] У прямокутного паралелепіпеда всі грані — прямокутники.[4] Довжини трьох ребер прямокутного паралелепіпеда, що мають спільну вершину, називають його вимірами.[1] Всі чотири діагоналі прямокутного паралелепіпеда рівні.[5] Моделями прямокутного паралелепіпеда може бути кімната, цеглина, сірникова коробка.
Куб — прямокутний паралелепіпед з рівними сторонами.[3] Всі шість граней куба — рівні квадрати.

Основні формули

Прямий паралелепіпед

Площа бічної поверхні:
$S б = Р о \cdot h$ , де $Р о$ — периметр основи, $h$ — висота.
Площа повної поверхні:
$S п = S б + 2 S о$ , де $S о$ — площа основи.
Об'єм паралелепіпеда дорівнює добутку площі його основи на висоту:
$V = S о \cdot h$ .

Прямокутний паралелепіпед

Площа бічної поверхні:
$S б = 2 c (a + b)$ , де $a$ , $b$ — сторони основи, $c$ — бічне ребро прямокутного паралелепіпеда.
Площа повної поверхні:
$S п = 2(ab + bc + ac)$ .
Об'єм:
$V = abc$ , де $a$ , $b$ , $c$ — виміри прямокутного паралелепіпеда.
У прямокутному паралелепіпеді квадрат діагоналі $d$ дорівнює сумі квадратів його вимірів:[5]
$d 2 = a 2 + b 2 + c 2$ .

Куб

Площа повної поверхні:
$S п = 6 a 2$ , де $a$ — сторона.
Об'єм:
$V = a 3$ .
Діагональ:
$d = a \sqrt 3$ .

Формули векторної алгебри

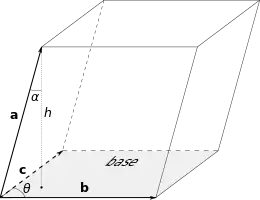
Паралелепіпед, який задається трьома векторами

a

,

b

і

c

.

Довжини векторних добутків

a \times b

і

b \times c

дорівнюють площам відповідних паралелограмів

Об'єм паралелепіпеда, побудованого на векторах $\mathbf {a} =(a_{1},a_{2},a_{3})$ , $\mathbf {b} =(b_{1},b_{2},b_{3})$ і $\mathbf {c} =(c_{1},c_{2},c_{3})$ розраховується як модуль мішаного добутку цих векторів:

V=\left|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )\right|=\left|\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )\right|=\left|\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} )\right|,

або

V=\left|\det {\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{bmatrix}}\right|.

Див. також

Примітки

Бевз, 2002, с. 110.
Погорелов, 2009, с. 73—75.
Киселёв, 1980, с. 211.
Крамор, 2008, с. 188.
Бевз, 2002, с. 112.

Література

Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія. Підручник для 10—11 класів загальноосвітніх навчальних закладів. — Київ : «Вежа», 2002. — ISBN 966-7091-31-7.
Погорелов А. В. Геометрия. 10—11 классы: учеб. для общеобразоват. учреждений. — 9-е изд. — Москва : Просвещение, 2009. — 175 с. — ISBN 978-5-09-021850-4.(рос.)
Крамор В. С. Повторяем и систематизируем школьный курс геометрии. — 4-е изд. — Москва : «Мир и Образование», 2008. — 336 с. — ISBN 978-5-94666-476-9.(рос.)
Киселёв А. П. Элементарная геометрия. Книга для учителя. — Москва : Просвещение, 1980. — 287 с.(рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTEБевз2002110-1] Бевз, 2002, с. 110.

[FOOTNOTEПогорелов200973—75-2] Погорелов, 2009, с. 73—75.

[FOOTNOTEКиселёв1980211-3] Киселёв, 1980, с. 211.

[FOOTNOTEКрамор2008188-4] Крамор, 2008, с. 188.

[FOOTNOTEБевз2002112-5] Бевз, 2002, с. 112.