Підмножина
Якщо X та Y — множини та будь-який елемент із X є також елементом із Y, то говорять, що:
- X є підмножиною (частиною) Y, позначення — X ⊆ Y;
- Y — надмножина (охоплююча множина) X, позначення — Y ⊇ X.
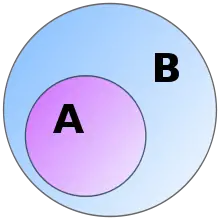
Кожна множина Y є підмножиною себе самої.
Підмножина Y, яка не збігається з Y називається точною підмножиною (або правильною чи власною частиною множини) Y.
Якщо X — точна підмножина Y, то цей факт записується як X ⊂ Y.
Відношення «бути підмножиною» має назву включення.
Варіанти позначень
Існують дві системи позначень відношень включення: старіша система використовує символ "⊂" для позначення будь-якої підмножини, і символ "⊊" для позначення точної підмножини. Нова система використовує "⊆" для позначення будь-якої підмножини, і "⊂" для позначення точної підмножини.
Власна підмножина
Із означення прямо слідує, що порожня множина мусить бути підмножиною будь-якої множини. Також, очевидно, будь-яка множина є своєю підмножиною:
- ∅ ⊂ B; B ⊆ B .
Якщо , і , то називається власною або нетривіа́льною підмножиною.
Приклади
- Множина {1, 2} є точною підмножиною {1, 2, 3}.
- Множина натуральних чисел є точною підмножиною множини раціональних чисел.
- Будь-яка множина є своєю підмножиною, але не точною.
- Порожня множина ∅ є також точною підмножиною будь-якої множини.
Властивості
ТВЕРДЖЕННЯ 1: Порожня множина є підмножиною всякої множини.
Доведення: Для довільної множини A потрібно довести, що ∅ є підмножиною A. Це рівнозначно тому, щоби показати, що всі елементиТ ∅ є також елементами A. Але в ∅ не існує жодного елемента.
Пояснимо: завдяки тому, що в ∅ немає елементів, "вони" не можуть бути нічиїми елементами. Тому для доведення зворотного, що ∅ не є підмножиною A, нам потрібно було б знайти такий елемент ∅, який не є одночасно елементом A. Таких елементів не існує (їх не існує взагалі), тому твердження 1 справедливе.
ТВЕРДЖЕННЯ 2: Якщо A, B та C є множини, тоді справедливі такі властивості відношення включення:
- рефлексивність:
- A ⊆ A
- антисиметричність:
- A ⊆ B та B ⊆ A тоді й тільки тоді, коли A = B
- транзитивність:
- Якщо A ⊆ B та B ⊆ C то A ⊆ C
Це твердження говорить про те, що множина X є алгебраїчною структурою, або решіткою, і якщо вона дистрибутивна (що показано в твердженні 1) та для кожного елементу існує його доповнення, то така структура має назву булевої алгебри.
ТВЕРДЖЕННЯ 3: Якщо A, B та C - підмножини S, то виконується наступне:
- існування верхньої межі та нижньої межі:
- Ø ⊆ A ⊆ S
- існування зв'язків:
- A ⊆ A ∪B
- Якщо A ⊆ C та B ⊆ C то A ∪B ⊆ C
- існування перетину:
- A ∩B ⊆ A
- Якщо C ⊆ A та C ⊆ B то C ⊆ A ∩B
ТВЕРДЖЕННЯ 4: Для будь-яких множин A та B, такі твердження еквівалентні:
- A ⊆ B
- A ∩B = A
- A ∪B = B
- A − B = Ø
- BC ⊆ AC
Посилання
- Thomas Jech (2002). Set Theory. Springer-Verlag. ISBN 3-540-44085-2.