Множина

Множина́ — одне з найважливіших понять сучасної математики. Поняття множини введено аксіоматично як сукупність певних об'єктів довільної природи, і тому множину не можна означити застосовуючи інші означені поняття. Навпаки, за допомогою поняття «множина» означають багато інших понять, і не лише в математиці. Об'єкти, які складають множину, називають елементами цієї множини. Наприклад, можна говорити про множину всіх книг у певній бібліотеці, множину літер українського алфавіту, або про множину всіх коренів певного рівняння тощо.

Основні поняття

Множину вважають визначеною (заданою), коли можна назвати чи «вказати» на всі ті об'єкти (елементи), які цій множині належать.

Множину позначають, як правило, великою літерою (часто жирним шрифтом), або переліком елементів цієї множини, записаним між фігурними дужками. Для деяких множин у математиці вживають усталені позначення. Наприклад:

  • Нехай А — множина. Символами «∈» та «∉» позначають відповідно «належність» та «неналежність» будь-якого елемента x множині А. Наприклад, x ∈ A (x належить А) або x ∉ A (x не належить А). Знак «∈» називають знаком належності. Він є стилізацією першої літери грецького слова εστι (бути).
  • Коли всі елементи множини В є елементами й множини А, то таку множину В називають підмножиною множини А. Для позначення того факту, що всі елементи множини B не є всіма елементами множини А, застосовують символи «⊂» та «⊃». Наприклад, B ⊂ A, A ⊃ B.
  • Якщо для множин А та B не задано відношень «йде за», тобто не задано відповідних способів, алгоритмів чи правил упорядкувань елементів цих множин, то множини А та B вважають рівними (позначають A = B) тоді, коли одночасно множина А є підмножиною множини В і множина В є підмножиною множини А, тобто тоді, коли всі елементи множини А є й всіма елементами множини В.
  • Для позначення того факту, що всі елементи множини B можуть бути чи є всіма елементами множини А, застосовують символи «⊆» та «⊇». Наприклад, B ⊆ A, A ⊇ B. Оскільки А є А, тобто А = А, то можна записувати, що 'A ⊆ A, або 'A ⊇ A. Символи «⊆», «⊇», «⊂», «⊃» називають символами включень.
  • У теорії множин виділяють також порожню множину, тобто множину, яка не містить жодного елемента. Таку множину позначають символом «∅». Порожня множина є підмножиною будь-якої множини.

Способи задання множин
  • Задання множини за допомогою переліку її елементів.

Нехай множина X містить елементи a, b, c, …, k. Для запису цього факту застосовують такий вираз:

X = {a, b, c, … , k}.

Приклади записів інших множин:

A = {4, 2, 1, 3},
B = {червоний, білий, блакитний},
ℕ = {1, 2, 3, … , n, …}.
  • Задання множини вказівкою властивості її елементів.

В математичних задачах, як правило, розглядають елементи деякої цілком означеної множини A. При цьому необхідні елементи виділяють за деякою їх властивістю (або вказують породжуючу процедуру) P, такою що кожний елемент x ∈ A або має властивість P (записується P(x)), або не має її. За допомогою властивості P виділимо множину всіх тих елементів, які мають властивість P. Цю множину будемо позначати як {x ∈ A | P(x)} = {x | P(x)}. Задання множини вказівкою її властивості (або породжуючим предикатом) слід здійснювати обережно. Наприклад, множина Y = {X|X∉X} (множина всіх множин, які не містять себе як елемента) веде до парадокса Рассела і є некоректною в аксіоматичній теорії множин.

Операції з множинами

Доповнення та різниця множин

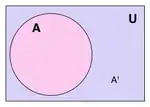
Нехай задана деяка множина U (універсальна множина або універсум). Якщо A ⊂ U, то елементи множини U, які не належать А, називаються доповненням множини А до множини U і позначають як CUA або UCA. Якщо A ⊂ U, B ⊂ U, то доповнення множини B до А називають різницею множин А та B (саме в такому порядку) і позначають А \ B або А-B, тобто A \ B = {x: x ∈ A ∧ x ∉ B}.

B мінус A
Різниця множин A та B
Доповнення A
Доповнення множини A до U
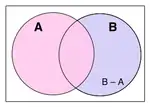
Примітка: Тут символ ∧ означає вимогу одночасної справедливості обох частин твердження (логічна зв'язка «І», кон'юнкція). Парний з ним символ ∨ означає вимогу справедливості щонайменше одного з двох тверджень (чи обох одночасно) (диз'юнкція, логічне АБО).

Приклади:

  • {1, 2} − {червоний, білий} = {1, 2}
  • {1, 2, зелений} − {червоний, білий, зелений} = {1, 2}
  • {1, 2} − {1, 2} = ∅
  • Якщо U — множина цілих чисел, то доповнення її підмножини A всіх парних чисел є підмножина В всіх непарних чисел.

Деякі властивості операції доповнення:

  • A ∪ A′ = U
  • A ∩ A′ = ∅
  • (A′)′ = A
  • A − B = A ∩ B′

Об'єднання множин
A union B
Об'єднання множин A та B

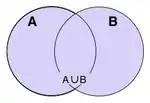
Об'єднанням множин А та B називається множина, яка складається з усіх тих елементів, які належать хоча б одній з множин A, B:

  • A ∪ B = {x: x ∈ A ∨ x ∈ B}.

Приклади:

  • {1, 2} ∪ {червоний, білий} = {1, 2, червоний, білий}
  • {1, 2, зелений} ∪ {червоний, білий, зелений} = {1, 2, червоний, білий, зелений}
  • {1, 2} ∪ {1, 2} = {1, 2}

Деякі властивості операції об'єднання:

  • A ∪ B   =   B ∪ A
  • A  ⊆  (A ∪ B)
  • A ∪ A   =  A
  • A ∪ ∅   =  A

Перетин множин
A intersect B
Перетин множин A та B

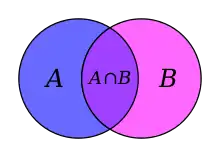
Перетином множин А та B називається множина, яка складається з усіх тих елементів, які належать кожній із множин А, B:

  • A ∩ B = {x: x ∈ A ∧ x ∈ B}.

Кажуть, що множини не перетинаються, якщо A ∩ B = ∅

Приклади:

  • {1, 2} ∩ {червоний, білий} = ∅
  • {1, 2, зелений} ∩ {червоний, білий, зелений} = {зелений}
  • {1, 2} ∩ {1, 2} = {1, 2}

Деякі властивості перетину:

  • A ∩ B   =   B ∩ A
  • A ∩ B   ⊆   A
  • A ∩ A   =   A
  • A ∩ ∅   =   ∅

Симетрична різниця множин

Симетрична різниця множин A та B є така множина елементів, які містяться в одній з цих двох множин, але не в обох. Позначається як AΔB.


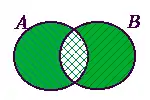
Симетрична різниця AΔB

Наприклад, симетрична різниця множин {1,2,3} та {3,4} є {1,2,4}.

Деякі властивості симетричної різниці:

A Δ B = (A − B) ∪(B − A)
A Δ B = (A ∪B) − (A ∩B)

Алгебра множин

Операції ∩, ∪ та доповнення множини утворюють алгебру з певними властивостями.

Потужність множини

Практично всі з розглянутих вище множин має визначену кількість елементів. Наприклад, множина А з розділу «Способи задання множин» має 4 елементи, множина B — три елементи. Порожня множина має нуль елементів. Існують множини, які мають нескінченну кількість елементів. Такою є множина ℕ всіх натуральних чисел. Поняття потужності множин стає важливим в контексті встановлення відношень між множинами. Зрозуміло, наприклад, що взаємооднозначне відношення між множинами А та B можливо встановити лише коли кількість їхніх елементів збігається. Особливо важливою проблема порівняння потужності постає для множин з нескінченною кількістю елементів. Виявляється, що потужності таких множин можуть бути не рівними, і це призводить до деяких цікавих наслідків.

Декартів добуток множин

Декартів добуток (прямий декартів добуток) множин X та Y — це множина усіх можливих впорядкованих пар або кортежів, першими компонентами яких є елементи множини X, а другими — елементи множини Y.

Декартів добуток множин X та Y позначається як X × Y: X × Y = { (x, y) | x ∈ X ∧ y ∈ Y }

Тут впорядкована пара (x, y) елементів x, y є множина {{x}, {x, y}}, яка має таку властивість, що (x, y) ≠ (y, x).

Див. також

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.