Редукція (паралельне програмування)

У OpenMP є оператор reduction:

reduction(+:sum)

Як і оператор private, він додається в конструкцію OpenMP, щоб повідомити компілятору, що слід очікувати редукції. Після цього створюється тимчасова закрита змінна, яка використовується для отримання проміжного результату операції підсумовування для кожного потоку. В кінці виконання конструкції значення цієї змінної для кожного потоку підсумовуються, щоб отримати кінцевий результат. Операція, яка використовується при редукції, також вказується в операторі. В даному випадку це операція "+". OpenMP визначає значення для закритої змінної, яка використовується в редукції, на основі відповідної математичної операції. Наприклад, для "+" це значення дорівнює нулю.

Нехай заданий масив a₀,a₁,...,a_n-1 і деяка бінарна асоціативна операція. Без обмеження спільності як операції далі буде розглядатися додавання. Тоді редукцією масиву a₀,a₁,...,a_n-1 щодо додавання називається:

A = (((a0+a1)+a2)+...+an-1)

Редукція тривіально реалізовується наступним послідовним кодом:

int sum = 0;
for(int i = 0; i < n; i++)
    sum += a[i];

• 
  Розділимо весь вихідний масив на частини, і кожній з них поставимо у відповідність один блок сітки блоків. Оскільки в CUDA максимальна розмірність блоку невелика (зазвичай 65535), великі одномірні масиви можуть бути необхідні для представлення як дво- або тривимірних, щоб збільшити діапазон індексації. Якщо в кожному блоці підсумувати тільки відповідну частину елементів масиву, то вихідна задача перетворюється в набір незалежних підзадач по знаходженню часткових сум. Для розпаралелювання кожної підзадачі по окремих нитках всередині блоку аналогічним чином продовжимо ділити підмасив спочатку на пари елементів, потім на пари їх часткових сум і так далі аж до однієї пари, що підсумовує дві половини підмасиву. Таким чином на кожному кроці підсумовуване число елементів зменшуватиметься удвічі, наприклад, у випадку 512 елементів у блоці буде потрібно log 512 = 9 кроків. Описаний процес для масиву з 16 елементів показаний на першому рисунку.
  
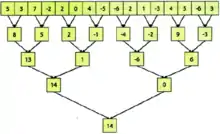  Підвищити ефективність доступу до пам`яті може попереднє копіювання відповідних елементів блоку в розділену пам`ять. У цьому випадку дані з повільної глобальної пам`яті будуть завантажені єдиний раз, і при знаходженні часткових сум буде використовуватися лише швидка розділена пам`ять. На другому рисунку показано відповідність потоків, елементів масиву і кроків підсумування для даного методу.

Приклад реалізації CUDA ядра на мові С:

__global__ void reduce1(int * inData, int * outData)
{
	__shared__ intdata[BLOCK_SIZE];
	int tid = threadIdx.x;
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	data[tid] = inData[i];		
	__syncthreads();
	for (int s = 1; s <blockDim.x; s *= 2)
	{
		if (tid % (2 * s) == 0)
			data[tid] += data[tid + s];
		__syncthreads();
	}
	if (tid == 0)					
		outData[blockIdx.x] = data[0];
}

• 
  Недоліком попереднього варіанту є велика кількість ітерацій циклу по s, в яких нитки одного варпу переходять в різні гілки умовного оператора. У цьому випадку всі нитки варпу виконують всі гілки. Викликані цим ефектом надлишкові обчислення можна виключити, перерозподіливши дані та операції, як це показано на третьому рисунку.

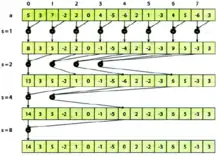
Код підповідного CUDA ядра:

__global__ void reduce2(int * inData, int * outData)
{
	__shared__ intdata[BLOCK_SIZE];
	Int tid = threadIdx.x;
	inti = blockIdx.x * blockDim.x + threadIdx.x;
	data[tid] = inData[i];		
	__syncthreads();
	for (int s = 1; s <blockDim.x; s <<= 1)
	{
		int index = 2 * s * tid;
		if (index<blockDim.x)
			data[index] += data[index + s];
		__syncthreads();
	}
	if (tid == 0)					
		outData[blockIdx.x] = data[0];
}

• 
  У другому варіанті ядра на кожному кроці циклу по s буде не більше одного варпу з розгалуженням, причому це розгалуження буде мати місце тільки для декількох останніх ітерацій циклу, а в інших випадках - на кордоні між варпами. Другий варіант також має недолік: при s = 2 всі звернення до пам`яті, що відповідають банкам з парними номерами, призводять до конфлікту банків 2-го порядку. Аналогічно, при s = 4 всі звернення відповідних банків з номерами 0, 4, 8, 12 призводять до конфлікту 4-го порядку і т.д. Таким чином, дана реалізація буде постійно приводити до конфліктів по банках високого порядку. Позбутися від конфліктів можна просто змінивши порядок вибору пар: замість вибору пари сусідніх елементів з подвоєнням відстані на кожній наступній операції, слід почати з пар елементів, що знаходяться на відстані BLOCKJSIZE /2, і на кожному кроці зменшувати відстань вдвічі, що показано на четвертому рисунку

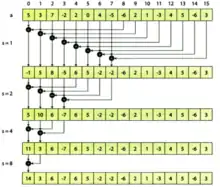
Нижче приведений код відповідного CUDA ядра:

__global__ void reduce3(int * inData, int * outData)
{
	__shared__ intdata[BLOCK_SIZE];
	inttid = threadIdx.x;
	inti = blockIdx.x * blockDim.x + threadIdx.x;
	data[tid] = inData[i];		
	__syncthreads();
	for (int s = blockDim.x / 2; s > 0; s >>= 1)
	{
		if (tid< s)
			data[tid] += data[tid + s];
		__syncthreads();
	}
	if (tid == 0)					
		outData[blockIdx.x] = data[0];
}

Глобальні і локальні операнди. Редукцію і сканування можна застосовувати до глобальних величин для отримання локально доступних результатів, наприклад: що призводить до отримання скалярного значення, що зберігається в локальній змінній least кожного потоку. Але редукція і сканування можуть також об'єднувати значення у множинних потоках. Операнди, тобто значення, що підлягають об'єднанню, можуть являти собою локальні змінні, а результат може бути присвоєно або локальній, або глобальній змінній. Таким чином, в операторі локальні змінні count, по одній в кожному потоці, об'єднуються, а один результат зберігається в локальній змінній total. Тобто кожен потік отримує копію результату.

Операції редукції і сканування. Використання в мові Peril-L похилої лінії і зворотньої похилої лінії, що розділяє оператор і операнд, для більшості програмістів незвично. У багатьох мовах використовується позначення у вигляді plus-reduce або min-scan, але таке позначення неможливо відрізнити від робочих викликів програмних функцій, воно затуманює важливість цих потужних абстракцій і знецінює їх роль. Ми спеціально вживаємо похилу риску, що бере початок в мові APL, щоб підкреслити важливість редукції і сканування.

Синхронізація редукції і сканування. Зверніть увагу, що оскільки операції редукції і сканування можуть працювати з множинними потоками, передбачається їх синхронізація, коли вони звертаються і привласнюють значення тільки до локальних змінних.

Для виконання підсумовування всі потоки повинні прибути до цього оператора, і жоден потік не може продовжувати роботу, поки привласнення не завершено. Тому привласнення або скороченої, або сканованою локальної величини локальної змінної має ефект бар'єрної синхронізації. Якщо результат зберігається в глобальній змінній, то як тільки потік внесе свою величину і виконає свою функцію в дереві операцій, він продовжить своє виконання.