Репер Дарбу

В диференціальній геометрії поверхонь, репер Дарбу — це природний рухомий репер, побудований на поверхні. Є аналогом тригранника Френе у геометрії поверхонь. Репер Дарбу існує в будь-який не омбілічній точці на поверхні в евклідовому просторі. Названий на честь французького математика Жана Гастона Дарбу.

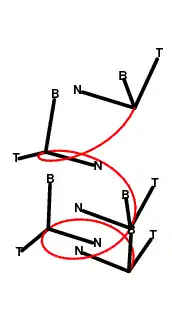
Тригранник Френе на кривій у просторі — це найпростіший приклад рухомої системи координат.

Репер Дарбу у точках вкладеної кривої

Нехай S — це орієнтована поверхня у тривимірному евклідовому просторі E³. Поняття репера Дарбу на поверхні S це по-перше рухомий репер, який пересувається вздовж кривої на поверхні S, а також уздовж напрямків головних кривин.

Геодезична кривина, нормальна кривина та геодезичний скрут

Нехай

\gamma \colon I\to {D^{2}}

внутрішнє рівняння кривої на регулярній поверхні S, параметризованій вектор-функцією

{\overrightarrow {r}}\colon {D^{2}}\to {E^{3}}

Тоді її зовнішнє рівняння, як кривої у E³ запишемо як композицію

{\overrightarrow {\gamma }}(t)=({\overrightarrow {r}}\circ \gamma )(t)

,

t\in I

Використовуючи правило диференціювання композицій відображення, знайдемо

{\overrightarrow {\gamma }}^{\prime }=\partial {\overrightarrow {r}}\cdot {\gamma }^{\prime }

Оберемо на кривій натуральну параметризацію: $\mid {\overrightarrow {\gamma }}^{\prime }\mid ={\sqrt {g({\gamma }^{\prime },{\gamma }^{\prime })}}\equiv 1$

Тоді ${\overrightarrow {\gamma }}^{\prime }$ являє собою одиничне дотичне векторне поле вздовж ${\overrightarrow {\gamma }}$ .

Якщо обмежити векторне поле нормалей поверхні на нашу криву, отримаємо векторне поле ${\overrightarrow {n}}(s)=({\overrightarrow {n}}\circ \gamma )$

Векторне поле ${\overrightarrow {\nu }}_{g}(s)={\overrightarrow {n}}(s)\times {\overrightarrow {\gamma }}^{\prime }(s)$ називають полем геодезичних нормалей кривої.

Трійку одиничних, взаємно ортогональних векторів ${\overrightarrow {\tau }}={\overrightarrow {\gamma }}^{\prime }(s),{\overrightarrow {\nu }}_{g}(s),{\overrightarrow {n}}(s)$ у точках кривої на поверхні називають репером Дарбу цієї кривої.

Розкладемо похідні по натуральному параметру векторних полів репера Дарбу по векторах цього ж репера. В силу одиничності розглянутих полів, отримаємо:

${\overrightarrow {\tau }}^{\prime }={e_{1}^{2}}{\overrightarrow {\nu }}_{g}+{e_{1}^{3}}{\overrightarrow {n}}$

${{\overrightarrow {\nu }}_{g}}^{\prime }={e_{2}^{1}}{\overrightarrow {\tau }}+{e_{2}^{3}}{\overrightarrow {n}}$

${\overrightarrow {n}}^{\prime }={e_{3}^{1}}{\overrightarrow {\tau }}+{e_{3}^{2}}{\overrightarrow {\nu }}_{g}$

Оскільки вектори репера Дарбу попарно ортогональні, то легко бачимо, що матриця коефіцієнтів такого розкладу кососиметрична, тобто ${e_{2}^{1}}=-e_{1}^{2},e_{3}^{1}=-e_{1}^{3},e_{3}^{2}=-e_{2}^{3}$ . А тому $e_{1}^{2},e_{1}^{3},e_{2}^{3}$ цілком визначають цей розклад.

Коефіцієнт $e_{1}^{3}$ називають геодезичною кривиною і позначаємо $k_{g}$ ;

Коефіцієнт $e_{2}^{3}$ називають нормальною кривиною і позначаємо $k_{n}$ ;

Коефіцієнт $e_{1}^{3}$ називають геодезичним скрутом і позначаємо $\varkappa _{g}$ ;

Див. також

Форма Маурера — Картана

Джерела

Guggenheimer, Heinrich (1977). Chapter 10. Surfaces. Differential Geometry. Dover. ISBN 0-486-63433-7.
Spivak, Michael (1999). A Comprehensive introduction to differential geometry (Volume 3). Publish or Perish. ISBN 0-914098-72-1.
Spivak, Michael (1999). A Comprehensive introduction to differential geometry (Volume 4). Publish or Perish. ISBN 0-914098-73-X.
Sternberg, Shlomo (1964). Lectures on differential geometry. Prentice-Hall.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.