Тригранник Френе

Тригранник або репер Френе — це природний рухомий репер у тривимірному просторі, що виникає на C³-гладкій кривій.

Тригранник Френе вздовж гвинтової лінії. Вектори ${\displaystyle \tau }$ — синій, ${\displaystyle \nu }$ — червоний, ${\displaystyle \beta }$ — чорний.

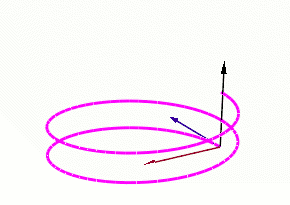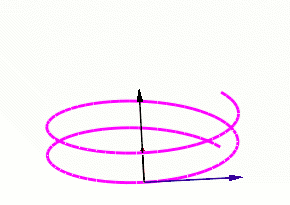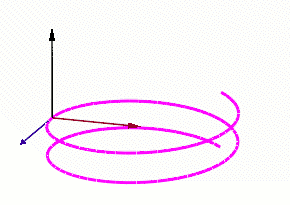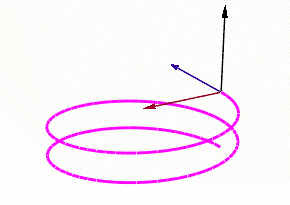
Нехай ${\displaystyle \gamma (t)}$ — C³-гладка крива в Евклідовому просторі ${\displaystyle \mathbb {E} ^{3}}$. Крива задана радіус-вектором ${\displaystyle r=r(s)}$, де s — натуральний параметр. З точкою ненульової кривини ${\displaystyle p\in \gamma (t),\ p=r(s)}$ можна зв'язати три вектори ${\displaystyle \tau (s),\nu (s),\beta (s),}$ які утворюють ортонормований базис. Де

${\displaystyle \tau ={\dot {r}}(s)}$ — одиничний дотичний вектор,

${\displaystyle \nu ={\frac {{\ddot {r}}(s)}{||{\ddot {r}}(s)||}}}$ — одиничний вектор головної нормалі,

${\displaystyle \beta =[\tau ,\nu ]}$  — одиничний вектор бінормалі до кривої в даній точці.

Вектори ${\displaystyle {\tau },{\nu },{\beta }}$ зв'язані співвідношеннями:

${\displaystyle {\begin{matrix}{\frac {d\tau }{ds}}&=&&k\nu &\\&&&&\\{\frac {d\nu }{ds}}&=&-k\tau &&+\,\varkappa \beta \\&&&&\\{\frac {d\beta }{ds}}&=&&-\varkappa \nu &\end{matrix}}}$

Величини

${\displaystyle k=||{\ddot {\gamma }}(s)||,\quad \varkappa =-\langle {\dot {\beta }},\;{\nu }\rangle }$

називають, відповідно, кривиною та скрутом кривої в даній точці. Рівняння виду ${\displaystyle k=f(s)\in C^{1},\ \kappa =g(s)\in C^{0},\,}$ де ${\displaystyle f(s)}$ усюди додатна називаються натуральними рівняннями кривої та визначають її з точністю до руху у просторі. Це твердження називають основною теоремою теорії кривих.

Формули Френе також відомі як теореми Френе, можна сформулювати, більш стисло, використовуючи матричні позначення:

${\displaystyle {\begin{bmatrix}\tau '\\\nu '\\\beta '\end{bmatrix}}={\begin{bmatrix}0&k&0\\-k&0&\varkappa \\0&-\varkappa &0\end{bmatrix}}{\begin{bmatrix}\tau \\\nu \\\beta \end{bmatrix}}.}$

Ця матриця буде кососиметричною.