Розбиття поверхні

Розбиття поверхні — метод, використовуваний у тривимірній комп'ютерній графіці, що представляє гладку поверхню за допомогою приблизної шматково-лінійної полігональної сітки. Гладка поверхня може бути зображена за допомогою приблизної сітки як границя рекурсивного поділу кожної полігональної грані на дрібніші грані, які краще апроксимують гладку поверхню.

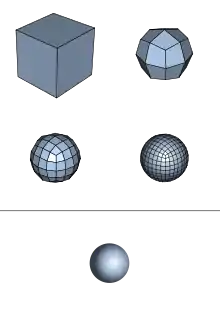
Перші три кроки розбиття куба із розбиттям поверхні внизу.

Загальне уявлення

Район поверхні визначається рекурсивно. Процес починається із заданої полігональної сітки. Потім до цієї сітки застосовується схема уточнення. Цей процес займає сітку і ділить її, створюючи нові вершини і нові грані. Позиції нових вершин в сітці обчислюються на основі позицій сусідніх вершин. У деяких схемах уточнення, позиції старих вершин також можуть бути змінені (на основі позицій нових вершин).

Цей процес виробляє більш дрібну сітку за оригінал, що містить більше полігональних меж. В результаті чого сітка може передаватися через ту саму схему уточнення знову і знову .

Поверхня граничного розбиття — поверхня, отримана з цього процесу, ітераційно може застосовуватися нескінченно багато разів. Однак в практичному використанні цей алгоритм застосовується обмежену кількість разів. Гранична поверхня також може бути обчислена безпосередньо для більшості підрозділів поверхонь із використанням техніки Джоза Стама[1], яка усуває необхідність у рекурсивному уточненні. Поєднані поверхні і Т-сплайни є конкуруючими технологіями. Математичні поверхні із розділенням є сплайн-поверхнями з особливостями.[2]

Схеми уточнення

Схеми удосконалення поверхонь підрозділів можуть бути в широкому сенсі розділені на дві категорії: інтерполяція та апроксимація. Інтерполяційні схеми необхідні, щоб відповідати вихідному положенню вершин у вихідній сітці. Апроксимаційні схеми — навпаки; Вони можуть і будуть коригувати ці позиції в міру необхідності. У цілому, апроксимаційні схеми мають велику гладкість, але редагування додатків, які дозволяють користувачам встановлювати точні поверхневі обмеження, вимагає оптимізації.

Існує ще один підрозділ в схемах розбиття поверхонь — тип полігону, на якому вони працюють. Деякі функції чотирикутників (квадроцикли), в той час як інші працюють на трикутниках.

Апроксимаційні схеми

Апроксимація означає, що граничні поверхні апроксимують початкові сітки і після розбиття новостворені контрольні точки не перебувають на граничних поверхнях. Прикладами схем розбиття є:

  • Кетмул-Кларк (1978) узагальнив бі-кубічний рівномірний B-сплайн, щоб зробити його уточнюючу схему. Для довільних початкових сіток, ця схема генерує граничні поверхні, які є безперервними С2 всюди, за винятком надзвичайних вершин, де вони є безперервними С1 (Петерс і Райф 1998).
  • Ду-Сабін — Друга схема розбиття була розроблена Ду та Сабіном (1978), яка успішно розширила метод кутового розрізання Чайкіна для кривих поверхонь. Вони використовували аналітичний вираз біквадратичної однорідної поверхні B-сплайнів для створення своєї процедури розбиття для отримання граничних поверхонь С1 з довільною топологією для довільних початкових сіток.
  • Loop, Triangles-Loop (1987) запропонували свою схему розбиття на основі сплайна четвертинного квадрата із шести направленими векторами, щоб забезпечити правило для генерації безперервних поверхонь C2 всюди, крім виняткових вершин, де вони безперервні по C1.
  • Схема підрозділу середнього краю. Схема підрозділу середнього краю була запропонована незалежно Петерсом-Рейфом (1997) і Хабіб-Уорреном (1999). Перший використовував середню точку кожного ребра, щоб побудувати нову сітку. Останній використовував сплайн з чотирма напрямками для побудови схеми. Ця схема породжує C1 безперервні граничні поверхні на початкових сітках із довільною топологією.
  • Схема розбиття √3 — Ця схема була розроблена Коббелтом (Kobbelt, 2000): вона обробляє довільні трикутні сітки, усюди неперервна, крім виняткових вершин, де вона C−1 переривається і при необхідності пропонує природну адаптивну обробку. Схема проявляє дві особливості: це подвійна схема для трикутних сіток та вона має більш повільну швидкість подрібнення, ніж первинна.

Схеми інтерполяції

Після розбиття контрольні точки вихідної сітки і нові згенеровані контрольні точки інтерполюються на граничну поверхню. Найбільш ранньою роботою була схема «метелики» Діна, Левіна і Грегорі (1990), яка розширила чотириточкову інтерполяційну схему розбиття кривих на схему розбиття поверхні. Зорін, Шредер і Свелденс (1996) помітили, що схема «метелики» не може генерувати гладкі поверхні для нерегулярних трикутних сіток і таким чином модифікувала цю схему. Коббальт (1996) додатково узагальнив чотириточкову інтерполяційну схему розбиття кривих на схему розподілу тензорного добутку поверхонь. Ден і Ма (2013) додатково узагальнили чотириточкову інтерполяційну схему розбиття на довільну ступінь.

  • Метелик, Трикутники — мають таку назву через форму схеми.
  • Середнє розбиття, Чотирикутники.
  • Коббальт, Чотирикутники — метод варіаційного розподілу, який намагається подолати рівномірні недоліки підрозділів.
  • Ден-Ма, Чотирикутники — 2n точкове розбиття, узагальнене на довільну непарну ступінь.[3]

Редагування поверхні розбиття

Поверхні підрозділу можуть бути природно відредаговані на різних рівнях підрозділу. Починаючи з базових форм, ви можете використовувати бінарні оператори для створення правильної топології. Потім відредагуйте грубу сітку, щоб створити базову фігуру, потім відредагуйте зміщення для наступного кроку поділу, а потім повторіть це на більш тонких рівнях. Ви завжди можете бачити як ваші зміни впливають на граничну поверхню за допомогою оцінки поверхні GPU.

Дизайнер поверхні також може починати з об'єкту сканування або об'єкту створеного з поверхні NURBS. Ті ж самі основні алгоритми оптимізації використовуються для створення грубої базової сітки з правильною топологією, а потім додають деталі на кожному рівні, щоб об'єкт можна було редагувати на різних рівнях. Із такими типами поверхонь може бути важко працювати, тому що базова сітка не має контрольних точок в тих місцях, куди розмістить їх дизайнер. Із відсканованого об'єкта з цією поверхнею легше працювати, ніж із сирою трикутною сіткою, але в об'єкта NURBS, ймовірно, були добре розкладені контрольні точки, які після конверсії поводяться менш інтуїтивно, ніж раніше.

Див. також

Ключові розробки
  • 1978: Поверхні розбиття були виявлені одночасно Едвіном Катмуллом і Джимом Кларком (див. Поверхня розбиття Кетмула-Кларка). У тому ж році Даніель Дуо і Малком Сабін опублікували паперовий макет за цією роботою (див. Поверхня розбиття Ду-Сабіна).
  • 1995: Ульріх Рейф характеризував поверхні поділу поблизу незвичайних вершин[4] by treating them as splines with singularities.[5], розглядаючи їх як сплайни з особливостями.
  • 1998: Джос Стам вніс свій внесок в метод точної оцінки поверхонь розбиття Кетмула-Кларка і Loop- розбиття при довільних значеннях параметрів.

Посилання
  1. Peters, J.; Reif, U. (October 1997). The simplest subdivision scheme for smoothing polyhedra. ACM Transactions on Graphics 16 (4): 420–431. doi:10.1145/263834.263851.
  2. Habib, A.; Warren, J. (May 1999). Edge and vertex insertion for a class C1 of subdivision surfaces. Computer Aided Geometric Design 16 (4): 223–247. doi:10.1016/S0167-8396(98)00045-4.
  3. http://dl.acm.org/citation.cfm?id=2487231
  4. Reif, U. (1995). A unified approach to subdivision algorithms near extraordinary vertices. Computer Aided Geometric Design 12 (2): 153–201. doi:10.1016/0167-8396(94)00007-F.
  5. Peters, J. R.; Reif, U. (2008). Subdivision Surfaces. Geometry and Computing 3. ISBN 978-3-540-76405-2. doi:10.1007/978-3-540-76406-9.
  • Peters, J.; Reif, U. (October 1997). The simplest subdivision scheme for smoothing polyhedra. ACM Transactions on Graphics 16 (4): 420–431. doi:10.1145/263834.263851.
  • Habib, A.; Warren, J. (May 1999). Edge and vertex insertion for a class C1 of subdivision surfaces. Computer Aided Geometric Design 16 (4): 223–247. doi:10.1016/S0167-8396(98)00045-4.
  • Kobbelt, L. (2000). √3-subdivision. Proceedings of the 27th annual conference on Computer graphics and interactive techniques - SIGGRAPH '00. с. 103–112. ISBN 1-58113-208-5. doi:10.1145/344779.344835.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.