Границя числової послідовності

Границя числової послідовності — фундаментальне поняття математичного аналізу, число, до якого члени послідовності прямують зі збільшенням індексу в сенсі наступного означення:

Послідовність представлена даними периметрами правильних багатокутників із n сторонами які описують одиничне коло при збільшенні кількості сторін має границю, яка дорівнює периметру кола, тобто

2\pi

. Відповідна послідовність вписаних багатокутників має ту саму границю при збільшенні кількості сторін n.

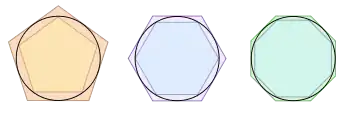
n	n sin(1/n)
1	0.841471
2	0.958851
…
10	0.998334
…
100	0.999983

Коли додатнє ціле число $n$ зростає, значення $n\cdot \sin {\bigg (}{\frac {1}{n}}{\bigg )}$ стає довільно близьким до $1$ . Тоді кажуть, що «границя послідовності $n\cdot \sin {\bigg (}{\frac {1}{n}}{\bigg )}$ дорівнює $1$ .»

Дійсне число a називається границею числової послідовності $\{a_{n}:n\geqslant 1\}$ , якщо $\forall \varepsilon >0\quad \exists N=N(\varepsilon )\in \mathbb {N} \quad \forall n\geqslant N:\;|a_{n}-a|<\varepsilon$ [1]

Позначення: $a=\lim _{n\to \infty }{a_{n}}$ або $a_{n}\to a,\quad n\to \infty$

При цьому також кажуть, що послідовність $\{a_{n}:n\geqslant 1\}$ збігається до числа a, або має границю a. Послідовність, що збігається до деякої границі називається збіжною, в інших випадках — розбіжною.

Історія

Грецький філософ Зенон Елейський відомий тим, що сформулював парадокси, що мають під собою процеси наближення до границі.

Левкіпп, Демокріт, Антіфон, Евдокс і Архімед розробили метод вичерпування, в яких використовують нескінченні послідовності для наближення, що дозволяли визначити площу або об'єм фігур. Архімед зміг розрахувати суми, що зараз називаються геометричними рядами.

Ньютон працював над рядами у своїх роботах Analysis with infinite series (укр. Аналіз нескінченних рядів, написана в 1669, поширювалася як рукопис і була опублікована в 1711), Метод флюксій і нескінченних рядів (укр. Аналіз нескінченних рядів, написана в 1671, опублікована у англійському перекладі в 1736, оригінал латиною було опубліковано набагато пізніше) і Tractatus de Quadratura Curvarum (написана в 1693, опублікована в 1704 як додаток до його Optiks). У своїй останній роботі, Ньютон розглядає біноміальне розкладання для (x + o)ⁿ, який він потім перетворює в лінійну форму за допомогою процедури розрахунку границі (задаючи, що o → 0).

В 18-му столітті, математики такі як Ейлер змогли успішно розрахувати суму деяких розбіжних рядів зупиняючи розрахунок в необхідний момент; вони не дуже турбувалися тим чи існує границя чи ні, доки це можна було розрахувати. Наприкінці століття, Лагранж в своїй роботі Théorie des fonctions analytiques (1797) стверджував, що відсутність суворості у понятті перешкоджає подальшому розвитку числення. Гаусс у своєму етюді про геометричний ряд (1813) вперше чітко дослідив за яких умов ряд буде збіжним до границі.

Сучасне визначення границі (для будь-якого ε при якому існує індекс N такий що …) сформулювали Бернард Больцано (в роботі Der binomische Lehrsatz, Прага 1816, що була мало помічена в той час) і Карл Вейєрштрасс в 1870-их.

Дійсні числа

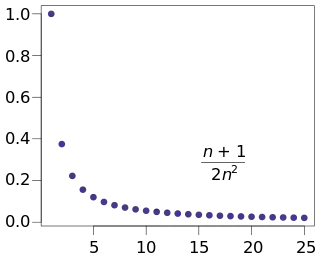
Графік послідовності {a_n}, що збігається показано синім. Наочно ми бачимо, що послідовність збігається до границі, що дорівнює 0 при зростанні n.

Для дійсних чисел, число $L$ є границею послідовності $(x_{n})$ якщо числа в цій послідовності стають все ближчими і ближчими до $L$ і більше ні до якого іншого числа.

Приклади

Якщо $x_{n}=c$ при сталому значенні c, тоді $x_{n}\to c$ .[Доказ 1]
Якщо $x_{n}={\frac {1}{n}}$ , тоді $x_{n}\to 0$ .[Доказ 2]
Для будь-якого даного дійсного числа, можна побудувати послідовність яка буде збігатися до даного числа за допомогою десяткового наближення. Наприклад, послідовність $0.3,0.33,0.333,0.3333,...$ буде збігатися до $1/3$ . Варто відмітити, що десяткове представлення $0.3333...$ є границею іншої послідовності, яка визначається наступним чином

0.3333...\triangleq \lim _{n\to \infty }\sum _{i=1}^{n}{\frac {3}{10^{i}}}

.

Процедура знаходження границі послідовності не завжди очевидна. Двома такими прикладами є $\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$ (границею якого є число e) і границя середнього арифметико-геометричного. Часто корисною для вирішення таких задач є стискна теорема.

Формальне визначення

$x$ називають границею числової послідовності $(x_{n})$ , якщо виконується наступна умова:

Для кожного дійсного числа $\epsilon >0$ , існує таке натуральне число $N$ таке що, для кожного натурального числа $n\geqslant N$ , будемо мати $|x_{n}-x|<\epsilon$ .

Іншими словами, для кожної міри близькості $\epsilon$ , елементи послідовності в кінцевому наближенні стають все ближчими до значення границі. Говорять, що послідовність $(x_{n})$ збігається до або прямує до границі $x$ , і це записується як $x_{n}\to x$ або $\lim _{n\to \infty }x_{n}=x$ .

Символічно, це матиме наступний вигляд:

$\forall \varepsilon >0(\exists N\in \mathbb {N} (\forall n\in \mathbb {N} (n\geqslant N\implies |x_{n}-x|<\varepsilon ))).$

Якщо послідовність збігається до деякої визначеної границі, тоді говорять що така послідовність є збіжною; в іншому випадку вона є розбіжною.

Ілюстрації

Приклад послідовності, що збігається до границі $a$ .
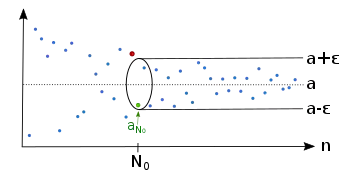Незалежно від того, наскільки мале число $\varepsilon >0$ , завжди існує такий індекс $N_{0}$ , що послідовність починаючи з цього індексу знаходиться повністю в околі точки $a$ радіусу $\varepsilon$ .
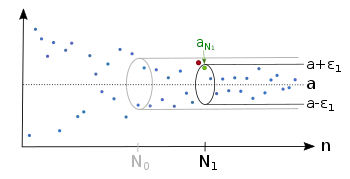А також для меншого значення $\varepsilon _{1}>0$ існує такий індекс $N_{1}$ , що послідовність починаючи з цього індексу знаходиться повністю в околі точки $a$ радіусу $\varepsilon _{1}$ .
Для кожного $\varepsilon >0$ існує лише обмежена кількість елементів послідовності, які знаходяться за межами околу точки $a$ радіусу $\varepsilon$ .

Властивості

Границі числових послідовностей дозволяють над собою застосовувати звичайні арифметичні операції. Якщо $a_{n}\to a$ і $b_{n}\to b$ , тоді $a_{n}+b_{n}\to a+b$ , $a_{n}\cdot b_{n}\to ab$ і, якщо ні b ні будь-яке з $b_{n}$ не дорівнюють нулю, ${\frac {a_{n}}{b_{n}}}\to {\frac {a}{b}}$ .

Для будь-якої неперервної функції f, якщо $x_{n}\to x$ тоді $f(x_{n})\to f(x)$ . Насправді, будь-яка функція f дійсних значень є неперервною тоді і тільки тоді, коли вона представляє собою границі послідовностей (хоча ця умова не завжди є необхідною, за умови застосування більш загального визначення неперервності).

Деякими іншими важливими властивостями границь послідовностей дійсних чисел є наступні (у кожному приведеному знизу рівнянні передбачається, що границі для правих частин виразів існують).

Границя послідовності є унікальною.
$\lim _{n\to \infty }(a_{n}\pm b_{n})=\lim _{n\to \infty }a_{n}\pm \lim _{n\to \infty }b_{n}$
$\lim _{n\to \infty }ca_{n}=c\cdot \lim _{n\to \infty }a_{n}$
$\lim _{n\to \infty }(a_{n}\cdot b_{n})=(\lim _{n\to \infty }a_{n})\cdot (\lim _{n\to \infty }b_{n})$
$\lim _{n\to \infty }\left({\frac {a_{n}}{b_{n}}}\right)={\frac {\lim \limits _{n\to \infty }a_{n}}{\lim \limits _{n\to \infty }b_{n}}}$ за умови, що $\lim _{n\to \infty }b_{n}\neq 0$
$\lim _{n\to \infty }a_{n}^{p}=\left[\lim _{n\to \infty }a_{n}\right]^{p}$
Якщо $a_{n}\leqslant b_{n}$ для всіх $n$ є більшою ніж деяке $N$ , тоді $\lim _{n\to \infty }a_{n}\leqslant \lim _{n\to \infty }b_{n}$
(Стискна теорема) Якщо $a_{n}\leqslant c_{n}\leqslant b_{n}$ для всіх $n>N$ , і $\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }b_{n}=L$ , тоді $\lim _{n\to \infty }c_{n}=L$ .
Якщо послідовність є обмеженою і монотонною тоді, вона є збіжною.
Послідовність є збіжною, якщо кожна з її підпослідовностей є збіжною.

Ці властивості часто використовуються для доведення існування границі без необхідності безпосередньо доводити громіздке початкове формальне визначення. Як тільки було доведено, що ${\frac {1}{n}}\to 0$ стає легко довести, що ${\frac {a}{b+{\frac {c}{n}}}}\to {\frac {a}{b}}$ , ( $b\neq 0$ ), використовуючи наведені вище властивості.

Нескінченні границі

Говорять, що послідовність $(x_{n})$ прямує до нескінченності, і позначають як $x_{n}\to \infty$ або $\lim _{n\to \infty }x_{n}=\infty$ якщо, для кожного K, існує таке N, що для кожного $n\geqslant N$ , $x_{n}>K$ ; тобто, елементи послідовності зрештою є більшими ніж будь-яке постійне значенняK. Аналогічно, $x_{n}\to -\infty$ якщо, для кожного K, існує таке N, що для кожного $n\geqslant N$ , $x_{n}<K$ . Якщо послідовність прямує до нескінченності, або до мінус нескінченності, то така послідовність є розбіжною (однак, розбіжна послідовність не обов'язково повинна прямувати до мінус чи плюс нескінченності: візьмемо наприклад $x_{n}=(-1)^{n}$ ).

Метричні простори

Визначення

Точка x метричного простору (X, d) є границею послідовності (x_n) якщо, для всіх ε > 0, існує таке N при якому, для будь-якого $n\geqslant N$ , $d(x_{n},x)<\epsilon$ . Це збігається із визначенням, що було дане для дійсних чисел коли $X=\mathbb {R}$ і $d(x,y)=|x-y|$ .

Властивості

Для будь-якої неперервної функції f, якщо $x_{n}\to x$ тоді $f(x_{n})\to f(x)$ . Насправді, функція f є неперервною тоді і тільки тоді, коли вона представляє собою границі послідовностей.

Границі послідовностей є унікальними, якщо вони існують, оскільки окремі взяті точки лежать окремо і мають деяку додатну міру відстані між ними, тому для $\epsilon$ що є меншим за половину цієї відстані, елементи послідовності не можуть бути в межах відстані $\epsilon$ для двох точок одночасно.

Топологічні простори

Визначення

Точка x топологічного простору (X, τ) є границею послідовності (x_n) якщо, для кожного околу U довкола x, існує таке N при якому, для кожного $n\geqslant N$ , $x_{n}\in U$ . Це збігається із визначенням, що було дане для метричних просторів, якщо (X,d) є метричним простором а $\tau$ є топологією утвореною за допомогою d.

Границя послідовності точок $\left(x_{n}:n\in \mathbb {N} \right)\;$ у топологічному просторі T є особливим випадком границі функції: областю визначення якої є $\mathbb {N}$ у просторі $\mathbb {N} \cup \lbrace +\infty \rbrace$ із індукованою топологією системи дійсних чисел розширеною до нескінченностей, ранг дорівнює T, а аргумент функції n прямує до +∞, яка в даному просторі є граничною точкою для $\mathbb {N}$ .

Властивості

Якщо X це Гаусдорфів простір тоді границі послідовностей є унікальними, якщо вони існують. Варто зазначити, що це не обов'язково так в загальному випадку; зокрема, якщо дві точки x і y є топологічно нерозрізнені, будь-яка послідовність яка збігається до x має збігатися до y і навпаки.

Послідовності Коші

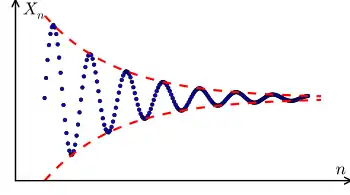
Графік фундаментальної послідовності Коші (x_n), показана синім, як x_n відносно n. Наочно, ми бачимо що послідовність збігається до граничної точки з тим як елементи послідовності стають ближчими один до одного із збільшенням n. В області дійсних чисел кожна послідовність Коші збігається до деякої границі.

Фундаментальна послідовність Коші, це така послідовність елементи якої врешті решт наближаються один до одного, після того як достатня кількість початкових елементів були відкинуті. Поняття послідовностей Коші є важливим при вивченні послідовностей в метричних просторах, і, зокрема, в аналізі функцій дійсної змінної. Одним із особливо важливим результатом в аналізі функцій дійсної змінної є критерій Коші щодо збіжності послідовностей: Послідовність дійсних чисел збігається тоді і тільки тоді, коли вона є послідовністю Коші. Цей критерій залишається достовірним і у інших повних метричних просторах.

Визначення для гіпердійсних чисел

Визначення границі, в якому застосовуються гіпердійсні числа формалізує інтуїтивне розуміння, що для «дуже великого» значення індекса послідовності, відповідний терм буде «дуже близьким» до границі. Точніше, послідовність дійсних чисел $(x_{n})$ прямує до L якщо для будь-якого нескінченного гіпернатурального, елемент x_H є нескінченно наближеним до L, тобто, різниця x_H − L є нескінченно малою величиною. Еквівалентно, L є стандартною частиною x_H

L={\rm {st}}(x_{H}).\,

Таким чином, границю можна визначити за допомогою наступної формули:

\lim _{n\to \infty }x_{n}={\rm {st}}(x_{H}),

Де границя існує тоді і тільки тоді, коли права частина є незалежною від вибору нескінченного H.

Література

Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Москва : Наука, 1962. — Т. 1. — 607 с.(рос.)
С. Т. Завало (1972). Елементи аналізу. Алгебра многочленів. Київ: Радянська школа.

Примітки

Дивіться математичний скоропис

Доведення

Доказ: нехай $N=1$ . Для кожного every $n\geqslant N$ , $|x_{n}-c|=0<\epsilon$
Доказ: нехай $N=\left\lfloor {\frac {1}{\epsilon }}\right\rfloor$ + 1 (ціла частина з округленням вниз). Для кожного $n\geqslant N$ , $|x_{n}-0|\leq x_{N}={\frac {1}{\lfloor 1/\epsilon \rfloor +1}}<\epsilon$ .

Див. також

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Дивіться математичний скоропис

[2] Доказ: нехай $N=1$ . Для кожного every $n\geqslant N$ , $|x_{n}-c|=0<\epsilon$

[3] Доказ: нехай $N=\left\lfloor {\frac {1}{\epsilon }}\right\rfloor$ + 1 (ціла частина з округленням вниз). Для кожного $n\geqslant N$ , $|x_{n}-0|\leq x_{N}={\frac {1}{\lfloor 1/\epsilon \rfloor +1}}<\epsilon$ .