Ромбокубооктаедр

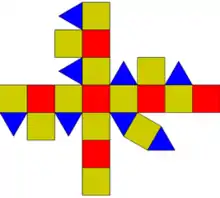
Ромбокубооктаедр[1] [2] [3] або ромбокубоктаедр [4] — напівправильний многогранник, гранями якого є 18 квадратів і 8 трикутників. Також називається малим ромбокубооктаедром [5].

Ромбокубооктаедр
Розгортка ромбокубооктаедра
Тривимірна модель ромбокубооктаедра

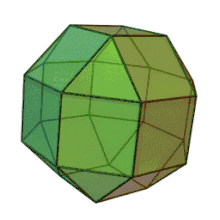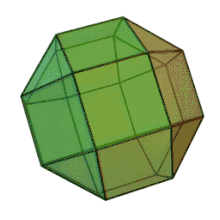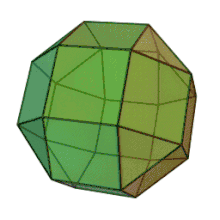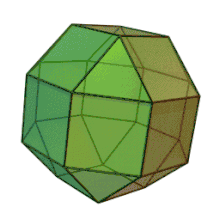
Алгебраїчні властивості

Декартові координати

Декартові координати вершин ромбокубооктаедра з центром на початку координат і довжиною ребер дорівнює двом — це все 24 можливі перестановки зі знаками наступної трійки: (± 1, ± 1, ± (1 + √2)).

Якщо вихідний ромбокубооктаедр має одиничні ребра, то довжини ребер двоїстого йому дельтоідального ікосітетраедра обчислюються за формулами:

Площа та об'єм

Площа S і об'єм V ромбокубооктаедра з довжиною ребра a, обчислюються за формулами.

Псевдоромбокубооктаедр

Повернувши верхню частину ромбокубооктаедр, що включає 5 квадратних і 4 трикутних грані, на кут 45 °, можна отримати новий багатогранник — псевдоромбокубооктаедр [6]. Псевдоромбокубооктаедр має рівні багатогранні кути, однак, щиро кажучи, не відноситься до архімедових багатогранників [6]; утім, його можна включити в список архімедових (або напівправильних) тіл, якщо виходити з менш жорсткого визначення: напівправильні (архімедові) багатогранники — багатогранники, всі багатогранні кути яких рівні, а всі грані — правильні багатокутники [7] [6] [8].

Псевдоромбокубооктаедр не був відомий протягом двох тисяч років [9] [10] і був виявлений в кінці 50-х — початку 60-х років двадцятого століття відразу декількома математиками, включаючи Дж. Міллера [11], радянського вченого В. Г. Ашкінузе (1957) [1] [12], югославського математика С. Білинського (1960) [13].

Приклади
Змійка Рубіка в формі близькій до ромбокубооктаедра
  • Ромбокубооктаедр добре відомий любителям головоломок: складеної в дуже схожий багатогранник часто продається знаменита змійка Рубика (на фото — частина квадратів замінена прямокутниками і трикутники замінені увігнуті з трьох прямокутних трикутників).
  • Будівля Національної бібліотеки Білорусі є ромбокубооктаедром висотою 73,6 м (23 поверхи) і вагою 115 000 тон (не рахуючи книг).
  • Ромбокубооктаедр зображений на єдиному відомому портреті Луки Пачолі.

Примітки
  1. Веннінджер, 1974.
  2. Болл, Коксетер, 1986.
  3. Люстерник, 1956, с. 183.
  4. Енциклопедія елементарної математики, +1963, с. 437, 435.
  5. Веннінджер, 1974, с. 12, 20.
  6. Веннінджер, 1974, с. 37.
  7. Веннінджер, +1974, с. 12.
  8. Болл, Коксетер, 1986, с. 449.
  9. Веннінджер, тисяча дев'ятсот сімдесят чотири.
  10. Люстерник, 1956.
  11. Болл, Коксетер, 1986, с. 152.
  12. Люстерник, 1956, с. 184-185.
  13. Веннінджер, тисячу дев'ятсот сімдесят чотири, с. 37.

Література
  • Веннінджер М. Моделі багатогранників / Пер. з англ. В. В. Фірсова. Під ред. і з послесл. І. М. Яглом. — 236 с.
  • Л. А. Люстерник. Опуклі фігури і многогранники.
  • Болл У., Коксетер Г. Математичні есе і розваги.
  • Багатокутники і багатогранники // Енциклопедія елементарної математики. Книга четверта. Геометрія / Под ред. П. С. Александрова, А. І. Маркушевича, А. Я. Хинчина.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.