Рівняння Чепмена — Колмогорова
Рівняння Чепмена-Колмогорова[1] — рівняння, що пов'язує умовні ймовірності для марківського процесу в різні моменти часу.
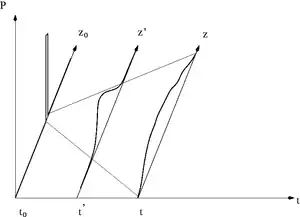
Еволюція функцій густини ймовірності в початковий момент часу (дельта), кінцевий момент часу та в деякий проміжковий момент .
Авторами рівняння є британський математик Сідні Чепмен та радянський математик Андрій Колмогоров.
Формулювання
Нехай — умовна функція густини ймовірності для марківського процесу (тобто ймовірність знайти випадкову змінну в інтервалі в момент часу за умови, що в момент часу дорівнює ). Тоді рівняння Чепмена-Колмогорова
пов'яже функції густини ймовірності в початковий момент часу , кінцевий момент часу та в деякий проміжковий момент .
Часто зустрічається запис рівняння Чепмена-Колмогорова через інтервали та . Тоді і рівняння Чепмена-Колмогорова набуває вигляду
Джерела
- Колмогоров А. Н. Основные понятия теории вероятностей. — М. : Наука, 1974. — 120 с.
Література
- Гардинер К. В. Стохастические методы в естественных науках. — М. : Мир, 1986. — 528 с.
- ван Кампен Н. Г. Стохастические процессы в физике и химии. — М. : Высшая школа, 1990. — 376 с.
- Либов Р. Введение в теорию кинетических уравнений. — М. : Мир, 1974. — 37 с.
- Хакен Г. Синергетика. — М. : Мир, 1980. — 406 с.
- Risken H. The Fokker-Planck Equation. — Berlin : Springer-Verlag, 1984.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
